Efficient gene orthology inference via large-scale rearrangements

Abstract

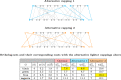
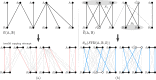
Background: Recently we developed a gene orthology inference tool based on genome rearrangements (Journal of Bioinformatics and Computational Biology 19:6, 2021). Given a set of genomes our method first computes all pairwise gene similarities. Then it runs pairwise ILP comparisons to compute optimal gene matchings, which minimize, by taking the similarities into account, the weighted rearrangement distance between the analyzed genomes (a problem that is NP-hard). The gene matchings are then integrated into gene families in the final step. The mentioned ILP includes an optimal capping that connects each end of a linear segment of one genome to an end of a linear segment in the other genome, producing an exponential increase of the search space.

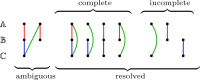
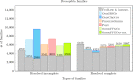
Results: In this work, we design and implement a heuristic capping algorithm that replaces the optimal capping by clustering (based on their gene content intersections) the linear segments into [Formula: see text] subsets, whose ends are capped independently. Furthermore, in each subset, instead of allowing all possible connections, we let only the ends of content-related segments be connected. Although there is no guarantee that m is much bigger than one, and with the possible side effect of resulting in sub-optimal instead of optimal gene matchings, the heuristic works very well in practice, from both the speed performance and the quality of computed solutions. Our experiments on primate and fruit fly genomes show two positive results. First, for complete assemblies of five primates the version with heuristic capping reports orthologies that are very similar to the orthologies computed by the version of our tool with optimal capping. Second, we were able to efficiently analyze fruit fly genomes with incomplete assemblies distributed in hundreds or even thousands of contigs, obtaining gene families that are very similar to [Formula: see text] families. Indeed, our tool inferred a higher number of complete cliques, with a higher intersection with [Formula: see text], when compared to gene families computed by other inference tools. We added a post-processing for refining, with the aid of the [Formula: see text] algorithm, our ambiguous families (those with more than one gene per genome), improving even more the accuracy of our results. Our approach is implemented into a pipeline incorporating the pre-computation of gene similarities and the post-processing refinement of ambiguous families with [Formula: see text]. Both the original version with optimal capping and the new modified version with heuristic capping can be downloaded, together with their detailed documentations, at https://gitlab.ub.uni-bielefeld.de/gi/FFGC or as a Conda package at https://anaconda.org/bioconda/ffgc .

Keywords: Comparative genomics; Double-cut-and-join; Gene orthology; Indels.

Fig. 1

On the top part is displayed the gene similarity graph $\mathcal{S}(\mathbb{A},\mathbb{B})$ of genomes $\mathbb{A}=\{[\mathtt{1}\mathtt{2}\mathtt{3}\mathtt{4}][\mathtt{5}\overline{\mathtt{6}}]\}$ and $\mathbb{B}=\{[\mathtt{7}\overline{\mathtt{8}}\overline{\mathtt{9}}\overline{\mathtt{10}}\mathtt{11}\mathtt{12}\mathtt{13}]\}$ and next to it a table with the ranking of four distinct ortholog-sets. On the middle the rearrangement scenarios induced by two of these ortholog-sets are shown. On the bottom part the family-free relational graph $FFR(\mathbb{A},\mathbb{B},\mathcal{S})$ is illustrated, highlighting the edges of the decomposition corresponding to the (black) ortholog-set $\mathcal{O}=\{\{\mathtt{1},\mathtt{7}\}$, $\{\mathtt{3},\mathtt{10}\},\{\mathtt{4},\mathtt{9}\},\{\mathtt{5},\mathtt{13}\}\}$. (This decomposition has two $\mathbb{A}\mathbb{B}$-paths, one $\mathbb{A}\mathbb{A}$-path and one cycle.) All extremity and indel edges in $FFR(\mathbb{A},\mathbb{B},\mathcal{S})$ are respectively scored and weighted according to $\mathcal{S}(\mathbb{A},\mathbb{B})$ but the scores and weights of edges not derived from $\mathcal{O}$ or $\tilde{\mathcal{O}}$ are omitted

Fig. 2

On the top part we show the capping of the decomposition corresponding to the (black) ortholog-set $\mathcal{O}=\{\{\mathtt{1},\mathtt{7}\}$, $\{\mathtt{3},\mathtt{10}\},\{\mathtt{4},\mathtt{9}\},\{\mathtt{5},\mathtt{13}\}\}$ from the gene similarity graph $\mathcal{S}(\mathbb{A},\mathbb{B})$ of Fig. 1 (bottom). Each red vertex is a cap vertex. Each filled (red) vertex is connected to a telomere (chromosome/path ends). The unfilled vertices represent the extra (equalizing) vertices connected by a dummy adjacency. The capping is a perfect matching of the complete bipartite graph of the cap vertices. The optimal capping for this decomposition is highlighted. It closes each of its paths into a separate cycle. (In general, an optimal capping of a decomposition may link up to 4 paths into a single cycle [8]). On the bottom part is displayed the complete family-free graph $FFR(\mathbb{A},\mathbb{B},\mathcal{S})$ optimally capped. Cap edges are unweighted. Scores of extremity edges and weights of indel edges are omitted

Fig. 3

Examples of two arbitrary lighter valid cappings of the family-free relational diagram from Fig. 1 (bottom) and their effects on the ranking of ortholog-sets/sibling-sets represented in Fig. 1 (top). Both cappings affect the computed distances, but, while the capping shown in the left (cyan) preserves the optimal ranking, the one shown in the right (orange) does not

Fig. 4

a Example of a shared-content graph $\mathcal{C}(\mathbb{A},\mathbb{B})$ with omitted edge scores. The genomes $\mathbb{A}$ and $\mathbb{B}$ have linear segments $A_{1..5}$ and $B_{1..5}$, respectively. The capping of $FFR(\mathbb{A},\mathbb{B},\mathcal{S})$ induced by $\mathcal{C}$ is invalid. b Transformation of $\mathcal{C}$ into a perfect shared-content graph $\widehat{\mathcal{C}}(\mathbb{A},\mathbb{B})$: vertex sets $S_1$ and $S_2$ represent Hall violators (among other possibilities) that demand the creation of dummy segments ${\phi }_{\mathbb{B}}^1$ and ${\phi }_{\mathbb{A}}^1$, respectively. Dotted edges represent those that are non-matchable and must be removed from $\widehat{\mathcal{C}}$ after the completion is finished. Notice that the component with vertices $A_1,A_2,A_3,B_1,{\phi }_{\mathbb{B}}^1\text{and}{B}_2$ is not a complete bipartite subgraph. (In both (a, b), we give an abstract illustration of the capped $FFR$ where only cap vertices, cap edges and dummy adjacencies are represented explicitly, while vertices of gene extremities between cap vertices are represented by a line with small dots. In addition, colored solid edges represent a maximum cardinality matching between cap vertices, while the cap edges not in the matching are dashed grey)

Fig. 5

The pipeline of our approach is straightforward: our gene families are the connected components of the n-partite graph derived by the integration of the computed ortholog-sets. The resulting ambiguous families can be optionally refined with the help of $\mathrm{M}\mathrm{C}\mathrm{L}$

Fig. 6

Types of families given by the integration of three ortholog-sets into a 3-partite graph

Fig. 7

The numbers of resolved incomplete and complete families in $\text{F}\mathrm{L}\mathrm{Y}\text{B}\mathrm{A}\mathrm{S}\mathrm{E}$, followed by the numbers of families inferred by $\mathrm{O}\mathrm{M}\mathrm{A}\mathrm{HOG}\mathrm{S}$, $\mathrm{O}\mathrm{M}\mathrm{A}\mathrm{G}\mathrm{R}\mathrm{O}\mathrm{U}\mathrm{P}\mathrm{S}$, $\text{P}\mathrm{R}\mathrm{O}\mathrm{T}\mathrm{E}\mathrm{I}\mathrm{N}\text{O}\mathrm{R}\mathrm{T}\mathrm{H}\mathrm{O}$, $\mathrm{P}\mathrm{O}\mathrm{F}\mathrm{F}$ and $\text{O}\mathrm{R}\mathrm{T}\mathrm{H}\mathrm{O}\text{FFGC}\approx$ (without and with $\mathrm{M}\mathrm{C}\mathrm{L}$ refinement). The lower part of each bar represents the intersection between the inferred sets and $\text{F}\mathrm{L}\mathrm{Y}\text{B}\mathrm{A}\mathrm{S}\mathrm{E}$. (For resolved complete families, the numbers of families in the intersections are shown on the top of bars)

Fig. 8

Precision $\left(\frac{\text{TP}}{\text{TP}+\text{FP}}\right)$, recall $\left(\frac{\text{TP}}{\text{TP}+\text{FN}}\right)$ and their harmonic mean $F_1$-score for $\mathrm{O}\mathrm{M}\mathrm{A}\mathrm{HOG}\mathrm{S}$, $\mathrm{O}\mathrm{M}\mathrm{A}\mathrm{G}\mathrm{R}\mathrm{O}\mathrm{U}\mathrm{P}\mathrm{S}$, $\text{P}\mathrm{R}\mathrm{O}\mathrm{T}\mathrm{E}\mathrm{I}\mathrm{N}\text{O}\mathrm{R}\mathrm{T}\mathrm{H}\mathrm{O}$, $\mathrm{P}\mathrm{O}\mathrm{F}\mathrm{F}$ and $\text{O}\mathrm{R}\mathrm{T}\mathrm{H}\mathrm{O}\text{FFGC}\approx$ (without and with $\mathrm{M}\mathrm{C}\mathrm{L}$ refinement), based on the dataset with eleven Drosophilas