This is a preprint.
Automated customization of large-scale spiking network models to neuronal population activity
- PMID: 37790533
- PMCID: PMC10542160
- DOI: 10.1101/2023.09.21.558920
Automated customization of large-scale spiking network models to neuronal population activity
Update in
-
Automated customization of large-scale spiking network models to neuronal population activity.Nat Comput Sci. 2024 Sep;4(9):690-705. doi: 10.1038/s43588-024-00688-3. Epub 2024 Sep 16. Nat Comput Sci. 2024. PMID: 39285002 Free PMC article.
Abstract
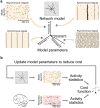
Understanding brain function is facilitated by constructing computational models that accurately reproduce aspects of brain activity. Networks of spiking neurons capture the underlying biophysics of neuronal circuits, yet the dependence of their activity on model parameters is notoriously complex. As a result, heuristic methods have been used to configure spiking network models, which can lead to an inability to discover activity regimes complex enough to match large-scale neuronal recordings. Here we propose an automatic procedure, Spiking Network Optimization using Population Statistics (SNOPS), to customize spiking network models that reproduce the population-wide covariability of large-scale neuronal recordings. We first confirmed that SNOPS accurately recovers simulated neural activity statistics. Then, we applied SNOPS to recordings in macaque visual and prefrontal cortices and discovered previously unknown limitations of spiking network models. Taken together, SNOPS can guide the development of network models and thereby enable deeper insight into how networks of neurons give rise to brain function.
Figures



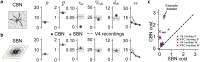

References
-
- Marder Eve and Bucher Dirk. Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu. Rev. Physiol., 69:291–316, 2007. - PubMed
-
- Vogels Tim P, Rajan Kanaka, and Abbott Larry F. Neural network dynamics. Annu. Rev. Neurosci., 28:357–376, 2005. - PubMed
-
- Kass Robert E, Amari Shun-Ichi, Arai Kensuke, Brown Emery N, Diekman Casey O, Diesmann Markus, Doiron Brent, Eden Uri T, Fairhall Adrienne L, Fiddyment Grant M, et al. Computational neuroscience: Mathematical and statistical perspectives. Annual review of statistics and its application, 5:183–214, 2018. - PMC - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
