Superconductivity in a breathing kagome metals ROs2 (R = Sc, Y, Lu)

Abstract

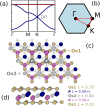
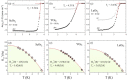
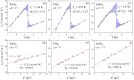
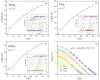
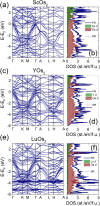
We have successfully synthesized three osmium-based hexagonal Laves compounds ROs₂ (R = Sc, Y, Lu), and discussed their physical properties. LeBail refinement of pXRD data confirms that all compounds crystallize in the hexagonal centrosymmetric MgZn₂-type structure (P6₃/mmc, No. 194). The refined lattice parameters are a = b = 5.1791(1) Å and c = 8.4841(2) Å for ScOs₂, a = b = 5.2571(3) Å and c = 8.6613(2) Å for LuOs₂ and a = b = 5.3067(6) Å and c = 8.7904(1) Å for YOs₂. ROs₂ Laves phases can be viewed as a stacking of kagome nets interleaved with triangular layers. Temperature-dependent magnetic susceptibility, resistivity and heat capacity measurements confirm bulk superconductivity at critical temperatures, T_c, of 5.36, 4.55, and 3.47 K for ScOs₂, YOs₂, and LuOs₂, respectively. We have shown that all investigated Laves compounds are weakly-coupled type-II superconductors. DFT calculations revealed that the band structure of ROs₂ is intricate due to multiple interacting d orbitals of Os and R. Nonetheless, the kagome-derived bands maintain their overall shape, and the Fermi level crosses a number of bands that originate from the kagome flat bands, broadened by interlayer interaction. As a result, ROs₂ can be classified as (breathing) kagome metal superconductors.

Figure 1

(a) 3-orbital tight-binding band structure of a kagome network with nearest-neighbor interactions only, showing a pair of Dirac bands crossing (DP) at the K point of the Brillouin zone. Locations of BZ points are shown schematically in (b). Crystal structure of ROs₂ (c,d) shown as a stacking of Os1 breathing kagome layers separated by triangular planes of R and Os2. Note that purple and gray triangles highlighted in panel (c) are not equal in size, thus the symmetry of the 2D kagome network is reduced from p6m to p3m1.

Figure 2

The unit cell volume vs the atomic radius ratio of the rare earth metal to osmium metal, r_R/r_Os. LaOs₂, CeOs₂, and PrOs₂ form in the hexagonal phase under high pressure.

Figure 3

Zero-field-cooled (open circles) and field-cooled (full circles) temperature-dependent magnetic susceptibility data (H = 10 Oe) for ScOs₂ (a), YOs₂ (b), and LuOs₂ (c). Temperature variation of the lower critical field for ScOs₂ (d), YOs₂ (e), and LuOs₂ (f).

Figure 4

Temperature dependence of the zero-field specific heat in the vicinity of the superconducting phase transition for ScOs₂ (a), YOs₂ (b), and LuOs₂ (c). C_p/T vs T² measured in a magnetic field: ScOs₂ (d), YOs₂ (e), and LuOs₂ (f).

Figure 5

The critical temperature, the Debye temperature, and the Sommerfeld coefficient versus atomic mass of the rare earth atom in ROs₂ compounds (R = Sc, Y and Lu).

Figure 6

The electrical resistivity versus temperature measured in zero applied magnetic field for ScOs₂ (a), YOs₂ (b), and LuOs₂ (c). Insets show the superconducting transition under various magnetic fields. (d) The temperature dependence of the upper critical field of all compounds, determined from electrical resistivity measurements.

Figure 7

Band structure and electronic density of states for ScOs₂ (a,b), YOs₂ (c,d), and LuOs₂ (e,f). In all three compounds the DOS(E_F) is dominated by the contribution of Os 5d states. Besides the splitting of the completely occupied 4f band in LuOs₂ (peak ca. − 4 to − 6 eV below the E_F), the difference between fully- (FR; blue line in panels b,d,f) and scalar-relativistic (SR; gray line) is rather small.

Figure 8

Band structure of ScOs₂ with Os1 d (a) and Os2 d (b) contribution highlighted (proportional to the color intensity). Os1 dominates the kagome-like bands between 0 and − 6 eV, while Os2 contributed mostly to a number of weakly dispersive bands between − 2 and − 3 eV. Panel (d) shows the tight binding band structure of a kagome system within 3 approximations: in the simplest case (thick gray lines) only nearest-neighbor interactions are considered and all the nearest neighbor tight binding hopping integrals are set to be equal (t_1, t₂ = − 1), resulting in a perfect p6m kagome. When the hexagonal symmetry is broken in breathing kagome (brown line; t₁ = − 1, t₂ = 0.9), the Dirac point at K is gapped, but the flat band remains intact. Inclusion of next-nearest neighbor interaction (orange line, t₁ = − 1, t₂ = 0.9, t₃ = 0.1) results in the flat band attaining some dispersion. The three tight-binding models are schematically drawn in panel (c).