Effects of Genetic Relatedness of Kin Pairs on Univariate ACE Model Performance

Abstract

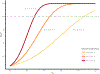
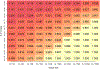
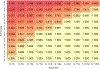
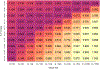
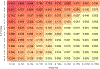
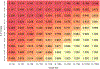
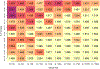
The current study explored the impact of genetic relatedness differences (ΔH) and sample size on the performance of nonclassical ACE models, with a focus on same-sex and opposite-sex twin groups. The ACE model is a statistical model that posits that additive genetic factors (A), common environmental factors (C), and specific (or nonshared) environmental factors plus measurement error (E) account for individual differences in a phenotype. By extending Visscher's (2004) least squares paradigm and conducting simulations, we illustrated how genetic relatedness of same-sex twins (H_SS) influences the statistical power of additive genetic estimates (A), AIC-based model performance, and the frequency of negative estimates. We found that larger H_SS and increased sample sizes were positively associated with increased power to detect additive genetic components and improved model performance, and reduction of negative estimates. We also found that the common solution of fixing the common environment correlation for sex-limited effects to .95 caused slightly worse model performance under most circumstances. Further, negative estimates were shown to be possible and were not always indicative of a failed model, but rather, they sometimes pointed to low power or model misspecification. Researchers using kin pairs with ΔH less than .5 should carefully consider performance implications and conduct comprehensive power analyses. Our findings provide valuable insights and practical guidelines for those working with nontwin kin pairs or situations where zygosity is unavailable, as well as areas for future research.

Keywords: ACE model; Sex limitation; Statistical power; Structural equation model; Twin design.

Figure 1.

This figure illustrates the power for detecting a significant a² parameter as a function of genetic relatedness of SS twins and variance combinations based on equation 3. We have fixed the sample size to 500 and set α to .05.

Figure 2–1.

Illustrates the power of the ACE model to detect A under the simulated variance of A = 1.5; C = .6; E = .9 (50%, 20%, 30%), as a function of sample size per twin group and H of SS twins. Power in each cell was calculated based on the average non-centrality parameter of 1000 simulations under the corresponding condition. Darker cell colors denote lower power.

Figure 2–2.

Illustrates the power of the ACE model to detect A under the simulated variance of A = 2.4; C = .3; E = .3, as a function of sample size per twin group and H of SS twins. Power in each cell was calculated based on the average non-centrality parameter of 1000 simulations under the corresponding condition. Darker cell colors denote lower power. ‘Sample size’ indicates the number of kin pairs in each kin group.

Figure 3.

Illustrates the proportion of the fitting results from 1000 simulated datasets where the ACE model has the lowest AIC compared to the AE and CE models. Simulated variance was set at A = 1.5; C = .6; E = .9 (50%, 20%, 30%), as a function of sample size per twin group and H of SS twins. Darker cell colors denote lower power. ‘Sample size’ indicates the number of kin pairs in each kin group.

Figure 4.

Illustrates the proportion of fitting results from 1000 simulated datasets with at least one negative estimate for A, C, or E variance components, when variance is set to A = 1.5; C = .6; E = .9 (50%, 20%, 30%), as a function of sample size per twin group and H of SS twins. Darker cell colors indicate higher prevalence of negative estimates. ‘Sample size’ indicates the number of kin pairs in each kin group.

Figure 5.

Displays the power of the ACE model to detect A under the simulated variance of A = 1.5; C = .6; E = .9 (50%, 20%, 30%) and the sex-limitation scalar of r_c = .95 included, as a function of sample size per twin group and H of SS twins. Power in each cell was calculated based on the average non-centrality parameter of 1000 simulations under the corresponding condition. Darker cell colors denote lower power. ‘Sample size’ indicates the number of kin pairs in each kin group.

Figure 6.

Average estimates of ‘A’ obtained from 1000 models, each fit to simulate data with variance combination A = 1.5, C = .6, E = .9 (50%, 20%, 30%). Darker cell colors denote larger deviations from the population parameter A = 1.5. ‘Sample size’ indicates the number of kin pairs in each kin group.