Co-embedding of edges and nodes with deep graph convolutional neural networks
- PMID: 37807013
- PMCID: PMC10560674
- DOI: 10.1038/s41598-023-44224-1
Co-embedding of edges and nodes with deep graph convolutional neural networks
Abstract
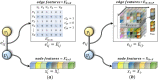
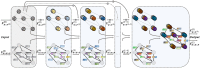
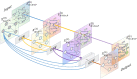
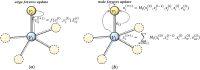
Graph neural networks (GNNs) have significant advantages in dealing with non-Euclidean data and have been widely used in various fields. However, most of the existing GNN models face two main challenges: (1) Most GNN models built upon the message-passing framework exhibit a shallow structure, which hampers their ability to efficiently transmit information between distant nodes. To address this, we aim to propose a novel message-passing framework, enabling the construction of GNN models with deep architectures akin to convolutional neural networks (CNNs), potentially comprising dozens or even hundreds of layers. (2) Existing models often approach the learning of edge and node features as separate tasks. To overcome this limitation, we aspire to develop a deep graph convolutional neural network learning framework capable of simultaneously acquiring edge embeddings and node embeddings. By utilizing the learned multi-dimensional edge feature matrix, we construct multi-channel filters to more effectively capture accurate node features. To address these challenges, we propose the Co-embedding of Edges and Nodes with Deep Graph Convolutional Neural Networks (CEN-DGCNN). In our approach, we propose a novel message-passing framework that can fully integrate and utilize both node features and multi-dimensional edge features. Based on this framework, we develop a deep graph convolutional neural network model that prevents over-smoothing and obtains node non-local structural features and refined high-order node features by extracting long-distance dependencies between nodes and utilizing multi-dimensional edge features. Moreover, we propose a novel graph convolutional layer that can learn node embeddings and multi-dimensional edge embeddings simultaneously. The layer updates multi-dimensional edge embeddings across layers based on node features and an attention mechanism, which enables efficient utilization and fusion of both node and edge features. Additionally, we propose a multi-dimensional edge feature encoding method based on directed edges, and use the resulting multi-dimensional edge feature matrix to construct a multi-channel filter to filter the node information. Lastly, extensive experiments show that CEN-DGCNN outperforms a large number of graph neural network baseline methods, demonstrating the effectiveness of our proposed method.
© 2023. Springer Nature Limited.
Conflict of interest statement
The authors declare no competing interests
Figures


Similar articles
-
MAMF-GCN: Multi-scale adaptive multi-channel fusion deep graph convolutional network for predicting mental disorder.Comput Biol Med. 2022 Sep;148:105823. doi: 10.1016/j.compbiomed.2022.105823. Epub 2022 Jul 6. Comput Biol Med. 2022. PMID: 35872410
-
A deep graph convolutional neural network architecture for graph classification.PLoS One. 2023 Mar 10;18(3):e0279604. doi: 10.1371/journal.pone.0279604. eCollection 2023. PLoS One. 2023. PMID: 36897837 Free PMC article.
-
Co-Embedding of Nodes and Edges With Graph Neural Networks.IEEE Trans Pattern Anal Mach Intell. 2023 Jun;45(6):7075-7086. doi: 10.1109/TPAMI.2020.3029762. Epub 2023 May 5. IEEE Trans Pattern Anal Mach Intell. 2023. PMID: 33052851
-
A Comprehensive Survey on Deep Graph Representation Learning.Neural Netw. 2024 May;173:106207. doi: 10.1016/j.neunet.2024.106207. Epub 2024 Feb 27. Neural Netw. 2024. PMID: 38442651 Review.
-
Graph neural networks in histopathology: Emerging trends and future directions.Med Image Anal. 2025 Apr;101:103444. doi: 10.1016/j.media.2024.103444. Epub 2025 Jan 7. Med Image Anal. 2025. PMID: 39793218 Review.
Cited by
-
The future of multimodal artificial intelligence models for integrating imaging and clinical metadata: a narrative review.Diagn Interv Radiol. 2025 Jul 8;31(4):303-312. doi: 10.4274/dir.2024.242631. Epub 2024 Oct 1. Diagn Interv Radiol. 2025. PMID: 39354728 Free PMC article. Review.
-
A message passing framework for precise cell state identification with scClassify2.Genome Biol. 2025 Aug 19;26(1):252. doi: 10.1186/s13059-025-03722-3. Genome Biol. 2025. PMID: 40830895 Free PMC article.
-
Using DeepSignalingFlow to mine signaling flows interpreting mechanism of synergy of cocktails.NPJ Syst Biol Appl. 2024 Aug 21;10(1):92. doi: 10.1038/s41540-024-00421-w. NPJ Syst Biol Appl. 2024. PMID: 39169016 Free PMC article.
References
-
- Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O. & Dahl, G. E. Neural message passing for quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning (eds. Precup, D. & Teh, Y. W.) vol. 70 1263–1272 (PMLR, 2017).
-
- Kipf, T. N. & Welling, M. Semi-supervised classification with graph convolutional networks. CoRRabs/1609.0 (2016).
-
- Duvenaud, D. et al. Convolutional networks on graphs for learning molecular fingerprints. In Advances in Neural Information Processing Systems 28: Annual Conference on Neural Information Processing Systems 2015, December 7–12, 2015, Montreal, Quebec, Canada (eds. Cortes, C., Lawrence, N. D., Lee, D. D., Sugiyama, M. & Garnett, R.) 2224–2232 (2015).
-
- Schlichtkrull, M. S. et al. Modeling relational data with graph convolutional networks. In The Semantic Web—15th International Conference, {ESWC} 2018, Heraklion, Crete, Greece, June 3–7, 2018, Proceedings (eds. Gangemi, A. et al.) vol. 10843, 593–607 (Springer, 2018).
-
- Veličković, P. et al. Graph attention networks. In 6th International Conference on Learning Representations, {ICLR} 2018, Vancouver, BC, Canada, April 30–May 3, 2018, Conference Track Proceedings (OpenReview.net, 2018).
Grants and funding
- No.U2268217/National Natural Science Foundation of China-China State Railway Group Co., Ltd. Railway Basic Research Joint Fund
- No.U2268217/National Natural Science Foundation of China-China State Railway Group Co., Ltd. Railway Basic Research Joint Fund
- No.U2268217/National Natural Science Foundation of China-China State Railway Group Co., Ltd. Railway Basic Research Joint Fund
- No.U2268217/National Natural Science Foundation of China-China State Railway Group Co., Ltd. Railway Basic Research Joint Fund
- No.U2268217/National Natural Science Foundation of China-China State Railway Group Co., Ltd. Railway Basic Research Joint Fund
- No.U2268217/National Natural Science Foundation of China-China State Railway Group Co., Ltd. Railway Basic Research Joint Fund
- No.2021YJ183/Scientific Funding for China Academy of Railway Sciences Corporation Limited
- No.2021YJ183/Scientific Funding for China Academy of Railway Sciences Corporation Limited
- No.2021YJ183/Scientific Funding for China Academy of Railway Sciences Corporation Limited
- No.2021YJ183/Scientific Funding for China Academy of Railway Sciences Corporation Limited
- No.2021YJ183/Scientific Funding for China Academy of Railway Sciences Corporation Limited
- No.2021YJ183/Scientific Funding for China Academy of Railway Sciences Corporation Limited
LinkOut - more resources
Full Text Sources

