Hot-spots detection in count data by Poisson assisted smooth sparse tensor decomposition

Abstract

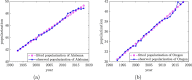
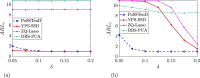
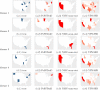
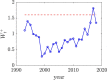
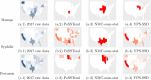
Count data occur widely in many bio-surveillance and healthcare applications, e.g. the numbers of new patients of different types of infectious diseases from different cities/counties/states repeatedly over time, say, daily/weekly/monthly. For this type of count data, one important task is the quick detection and localization of hot-spots in terms of unusual infectious rates so that we can respond appropriately. In this paper, we develop a method called Poisson assisted Smooth Sparse Tensor Decomposition (PoSSTenD), which not only detect when hot-spots occur but also localize where hot-spots occur. The main idea of our proposed PoSSTenD method is articulated as follows. First, we represent the observed count data as a three-dimensional tensor including (1) a spatial dimension for location patterns, e.g. different cities/countries/states; (2) a temporal domain for time patterns, e.g. daily/weekly/monthly; (3) a categorical dimension for different types of data sources, e.g. different types of diseases. Second, we fit this tensor into a Poisson regression model, and then we further decompose the infectious rate into two components: smooth global trend and local hot-spots. Third, we detect when hot-spots occur by building a cumulative sum (CUSUM) control chart and localize where hot-spots occur by their LASSO-type sparse estimation. The usefulness of our proposed methodology is validated through numerical simulation studies and a real-world dataset, which records the annual number of 10 different infectious diseases from 1993 to 2018 for 49 mainland states in the United States.

Keywords: CUSUM; Hot-spots detection; Poisson regression; spatio-temporal model; tensor decomposition.

Figure 1.

Data visualization of our motivating dataset. (a) bar plot of 10 diseases. (b) map of 49 states. (c) time series of 26 years.

Figure 2.

The pipeline of our algorithm to minimize $F({\mathit{\theta }}_m,{\mathit{\theta }}_h)$ with respect to ${\mathit{\theta }}_m,{\mathit{\theta }}_h$.

Figure 3.

Population and estimate in Alabama and Georgia during 1993–2018. (a) Alabama. (b) Oregon.

Figure 4.

The ${\mathrm{ARL}}_1$ plot of our proposed PoSSTenD method, and the three benchmark methods, i.e. YPS-SSD method, ZQ-Lasso method and DBS-PCA method. (a) population with an increasing trend. (b) population with a decreasing trend.

Figure 5.

Comparison of true hot-spots and hot-spots detected by our PoSSTenD method and YPS-SSD method under the decreasing population size and large hot-spots $\delta =0.2$. (a.1) true. (a.2) PoSSTenD. (a.3) NMC-scan-stat & (a.4) YPS-SSD (b.1) true. (b.2) PoSSTenD. (b.3) NMC-scan-stat. (b.4) YPS-SSD (c.1) true. (c.2) PoSSTenD. (c.3) NMC-scan-stat. (c.4) YPS-SSD (d.1) true. (d.2) PoSSTenD. (d.3) NMC-scan-stat. (d.4) YPS-SSD (e.1) true & (e.2) PoSSTenD. (e.3) NMC-scan-stat. (e.4) YPS-SSD.

Figure 6.

Control chart of our proposed method.

Figure 7.

Hot-spots detection result of mumps, syphilis and pertussis in 2017 by our proposed PoSSTenD method (second column), NMC-scan-stat (third column) and YPS-SSD method (last column). The first column is the raw data of the number of infected people of mumps, syphilis and pertussis in 2017. (a.1) 2017 raw data. (a.2) PoSSTend. (a.3) NMC-scan-stat. (a.4) YPS-SSD (b.1) 2017 raw data. (b.2) PoSSTend. (b.3) NMC-scan-stat. (b.4) YPS-SSD (c.1) 2017 raw data. (c.2) PoSSTend. (c.3) NMC-scan-stat. (c.4) YPS-SSD.