Significance testing of rank cross-correlations between autocorrelated time series with short-range dependence

Abstract

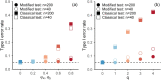
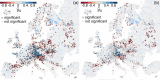
Statistical dependency measures such as Kendall's Tau or Spearman's Rho are frequently used to analyse the coherence between time series in environmental data analyses. Autocorrelation of the data can, however, result in spurious cross correlations if not accounted for. Here, we present the asymptotic distribution of the estimators of Spearman's Rho and Kendall's Tau, which can be used for statistical hypothesis testing of cross-correlations between autocorrelated observations. The results are derived using U-statistics under the assumption of absolutely regular (or β-mixing) processes. These comprise many short-range dependent processes, such as ARMA-, GARCH- and some copula-based models relevant in the environmental sciences. We show that while the assumption of absolute regularity is required, the specific type of model does not have to be specified for the hypothesis test. Simulations show the improved performance of the modified hypothesis test for some common stochastic models and small to moderate sample sizes under autocorrelation. The methodology is applied to observed climatological time series of flood discharges and temperatures in Europe. While the standard test results in spurious correlations between floods and temperatures, this is not the case for the proposed test, which is more consistent with the literature on flood regime changes in Europe.

Keywords: Kendall’s Tau; Spearman’s Rho; autocorrelation; significance testing; $\beta$-mixing.

Figure 1.

(a) Realization of a bivariate VAR(1)-process $X_t$ with Gaussian noise, normal marginal distributions, individual AR(1)-parameters of 0.8, but no dependence between the components. Estimate of Spearman’s Rho for the sample at the top left of the panel. (b) Asymptotic distribution of the estimator of Spearman’s Rho ${\rho }_S$ under ${\mathcal{H}}_0$ (no pairwise dependence) for independent observations. (c) Asymptotic distribution of the estimator of Spearman’s Rho under ${\mathcal{H}}_0$ for dependent observations (see Corollary 2.1). In panels (b) and (c) the critical region for the corresponding significance test at $\alpha =0.05$ are highlighted, and the sample-estimate of Spearman’s Rho for the trajectory in panel (a) is depicted as a circle.

Figure 2.

Observed type 1 error rate for two-sided significance test of Spearman’s Rho for Model 1 (panel a) and Model 2 (panel b) at α = 0.05 based on simulations (10,000 runs). Horizontal axes represent the parameters of the models governing the autocorrelations of the components ( ${\phi }_X={\phi }_Y$ and $\nu =4$ for all results shown here), shapes indicate which asymptotic distribution was used for the significance test, i.e. Squares: classical test; Circles: modified test. Open symbols: n = 40, Full symbols: n = 200.

Figure 3.

Observed power for two-sided significance tests of Spearman’s Rho for Model 1 (equations 7.1 & 7.2) and different sample sizes at α = 0.05 based on simulations (10,000 runs). Panels refer to results for different values of the parameter $\rho$ of Model 1. Horizontal axes represent sample size. ${\phi }_X={\phi }_Y$ for all results shown here. Shapes indicate which asymptotic distribution was used for the significance test, i.e. (Open squares) classical test, (Full circles) modified test.

Figure 4.

Observed power for two-sided significance tests of Spearman’s Rho for Model 2 (equations 7.3 & 7.4) and different sample sizes at α = 0.05 based on simulations (10,000 runs). Panels refer to results for different values of the parameter $\rho$ of Model 2 ( $\nu =4$). Horizontal axes represent sample size. Shapes indicate which asymptotic distribution was used for the significance test, i.e. (Open squares) classical test, (Full circles) modified test.

Figure 5.

Estimated Spearman-correlations between annual series of flood peak discharges and average annual catchment temperatures. All series are smoothed via a two-sided moving average filter of length 5 with equal weights, centred at the observations (similar to Model 2 with $q=2$). The circles, representing catchments, indicate the magnitude of the estimated Spearman correlations. The size and the transparency of the circles indicate statistical significance at α = 0.05. Panel (a) depicts results of the classical test, panel (b) those of the modified test. Flood data from [4], temperature data from E-OBS, see [14].