Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Sep 26:9:e1579.
doi: 10.7717/peerj-cs.1579. eCollection 2023.

A spatially variant high-order variational model for Rician noise removal

Tran Dang Khoa Phan  1
Affiliations

A spatially variant high-order variational model for Rician noise removal

Tran Dang Khoa Phan. PeerJ Comput Sci. .

Abstract

Rician noise removal is an important problem in magnetic resonance (MR) imaging. Among the existing approaches, the variational method is an essential mathematical technique for Rician noise reduction. The previous variational methods mainly employ the total variation (TV) regularizer, which is a first-order term. Although the TV regularizer is able to remove noise while preserving object edges, it suffers the staircase effect. Besides, the adaptability has received little research attention. To this end, we propose a spatially variant high-order variational model (SVHOVM) for Rician noise reduction. We introduce a spatially variant TV regularizer, which can adjust the smoothing strength for each pixel depending on its characteristics. Furthermore, SVHOVM utilizes the bounded Hessian (BH) regularizer to diminish the staircase effect generated by the TV term. We develop a split Bregman algorithm to solve the proposed minimization problem. Extensive experiments are performed to demonstrate the superiority of SVHOVM over some existing variational models for Rician noise removal.

Keywords: Bounded Hessian; Image denoising; Magnetic resonance imaging; Rician noise; Split Bregman; Total variation; Variational method.

PubMed Disclaimer

Conflict of interest statement

The authors declare there are no competing interests.

Figures

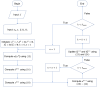
Figure 1
Figure 1. The flowchart of the split Bregman algorithm for solving the proposed problem (11).
The parameters kmax and nmax denote the outer and inner iteration numbers, respectively.
Figure 2
Figure 2. Sample MR images.
Image source credit: IXI dataset, CC BY-SA 3.0 (https://brain-development.org/ixi-dataset/).
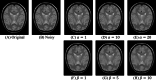
Figure 3
Figure 3. The effects of the paramerters α0 and β for an image of the IXI dataset at the noise level σ = 15: (C)–(E) for the fixed β = 1; (F)–(H) for the fixed α0 = 15.
Image source credit: IXI dataset, CC BY-SA 3.0 (https://brain-development.org/ixi-dataset/).
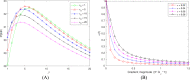
Figure 4
Figure 4. The effects of the parameters α0, β, and κ. (A) The PSNR values under different α0 and β settings at the noise level σ = 15; (B) The effect of the contrast parameter κ on the weighting function α(⋅).
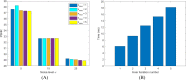
Figure 5
Figure 5. The dependence of SVHOVM’s performance on the inner iteration number for: (A) The PSNR values; (B) The average time per iteration. The outer iteration number kmax is fixed by 500; the inner iteration number nmax is set to 1, 2, .., 5.
The noise levels σ = 5, 15,  and 25 are considered.
Figure 6
Figure 6. Denoising results of different models on an image of the IXI dataset with the noise level σ = 5.
The parts of the denoised images, which are framed by green boxes, are enlarged for visual comparison. The 1D curves of intensity value are shown below the denoised images. Image source credit: IXI dataset, CC BY-SA 3.0 (https://brain-development.org/ixi-dataset/).
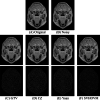
Figure 7
Figure 7. Denoising results of different models on an image of the IXI dataset with the noise level σ = 15 and the associated residual images Image source credit: IXI dataset, CC BY-SA 3.0 (https://brain-development.org/ixi-dataset/).
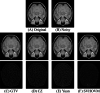
Figure 8
Figure 8. Denoising results of different models on an image of the IXI dataset with the noise level σ = 25 and the associated residual images.
Image source credit: IXI dataset, CC BY-SA 3.0 (https://brain-development.org/ixi-dataset/).
See this image and copyright information in PMC

References

    1. Aja-Fernández S, Alberola-López C, Westin C-F. Noise and signal estimation in magnitude MRI and Rician distributed images: a LMMSE approach. IEEE Transactions on Image Processing. 2008;17(8):1383–1398. doi: 10.1109/TIP.2008.925382. - DOI - PubMed
    1. Aja-Fernández S, Vegas-Sánchez-Ferrero G. Statistical analysis of noise in MRI, Modeling, Filtering and Estimation. Cham: Springer; 2016. - DOI
    1. Baselice F, Ferraioli G, Pascazio V, Sorriso A. Denoising of MR images using Kolmogorov-Smirnov distance in a non local framework. Magnetic Resonance Imaging. 2019;57:176–193. doi: 10.1016/j.mri.2018.11.022. - DOI - PubMed
    1. Bernstein M, Thomasson DM, Perman WH. Improved detectability in low signal-to-noise ratio magnetic resonance images by means of a phase-corrected real reconstruction. Medical Physics. 1989;16(5):813–817. doi: 10.1118/1.596304. - DOI - PubMed
    1. Bertsekas DP. Constrained optimization and Lagrange multiplier methods. Academic press; New York: 2014.

LinkOut - more resources