Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Sep 29:2023:6908757.
doi: 10.1155/2023/6908757. eCollection 2023.

Analysis of HBV and COVID-19 Coinfection Model with Intervention Strategies

Shewafera Wondimagegnhu Teklu  1
Affiliations

Analysis of HBV and COVID-19 Coinfection Model with Intervention Strategies

Shewafera Wondimagegnhu Teklu. Comput Math Methods Med. .

Abstract

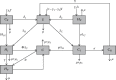
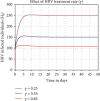
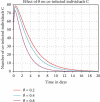
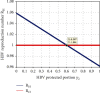
Coinfection of hepatitis B virus (HBV) and COVID-19 is a common public health problem throughout some nations in the world. In this study, a mathematical model for hepatitis B virus (HBV) and COVID-19 coinfection is constructed to investigate the effect of protection and treatment mechanisms on its spread in the community. Necessary conditions of the proposed model nonnegativity and boundedness of solutions are analyzed. We calculated the model reproduction numbers and carried out the local stabilities of disease-free equilibrium points whenever the associated reproduction number is less than unity. Using the well-known Castillo-Chavez criteria, the disease-free equilibrium points are shown to be globally asymptotically stable whenever the associated reproduction number is less than unity. Sensitivity analysis proved that the most influential parameters are transmission rates. Moreover, we carried out numerical simulation and shown results: some parameters have high spreading effect on the disease transmission, single infections have great impact on the coinfection transmission, and using protections and treatments simultaneously is the most effective strategy to minimize and also to eradicate the HBV and COVID-19 coinfection spreading in the community. It is concluded that to control the transmission of both diseases in a population, efforts must be geared towards preventing incident infection with either or both diseases.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no conflicts of interest

Figures

Figure 1
Figure 1
The flow chart of the coinfection of HBV and COVID-19 spreading dynamics with λH(t) and λC(t) given in (1) and (2), respectively.
Figure 2
Figure 2
Simulation of sensitivity indices of the model parameters with respect to ℛHC0.
Figure 3
Figure 3
Convergence of the complete coinfection dynamics (3) solutions at ℛHC0 = 0.26 < 1.
Figure 4
Figure 4
Convergence of the complete coinfection dynamics (3) solutions at ℛHC0 = 3.23 > 1.
Figure 5
Figure 5
Impact of σ1 on C.
Figure 6
Figure 6
Impact of σ2 on C.
Figure 7
Figure 7
Impact of γ on HI.
Figure 8
Figure 8
Impact of θ on C.
Figure 9
Figure 9
Impact of σ1 on ℛH.
Figure 10
Figure 10
Impact of γ2 on ℛH.
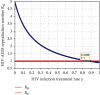
Figure 11
Figure 11
Impact of γ on ℛH.
Figure 12
Figure 12
Impact of σ2 on ℛC.
Figure 13
Figure 13
Impact of γ1 on ℛC.
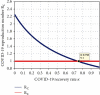
Figure 14
Figure 14
Impact of κ on ℛC.
See this image and copyright information in PMC

References

    1. Din A., Amine S., Allali A. A stochastically perturbed co-infection epidemic model for COVID-19 and hepatitis B virus. Nonlinear Dynamics . 2023;111(2):1921–1945. - PMC - PubMed
    1. Martcheva M. An Introduction to Mathematical Epidemiology . Vol. 61. New York: Springer; 2015. - DOI
    1. Omame A., Abbas M., Onyenegecha C. P. A fractional order model for the co-interaction of COVID-19 and hepatitis B virus. Results in Physics . 2022;37, article 105498 doi: 10.1016/j.rinp.2022.105498. - DOI - PMC - PubMed
    1. Khatun Z., Islam M. S., Ghosh U. Mathematical modeling of hepatitis B virus infection incorporating immune responses. Sensors International . 2020;1, article 100017 doi: 10.1016/j.sintl.2020.100017. - DOI
    1. Liang P., Jian Z., Zhuang G. A literature review of mathematical models of hepatitis B virus transmission applied to immunization strategies from 1994 to 2015. Journal of Epidemiology . 2018;28(5):221–229. doi: 10.2188/jea.JE20160203. - DOI - PMC - PubMed