Semilocal Meta-GGA Exchange-Correlation Approximation from Adiabatic Connection Formalism: Extent and Limitations
- PMID: 37811903
- PMCID: PMC10591512
- DOI: 10.1021/acs.jpca.3c03976
Semilocal Meta-GGA Exchange-Correlation Approximation from Adiabatic Connection Formalism: Extent and Limitations
Abstract
The incorporation of a strong-interaction regime within the approximate semilocal exchange-correlation functionals still remains a very challenging task for density functional theory. One of the promising attempts in this direction is the recently proposed adiabatic connection semilocal correlation (ACSC) approach [Constantin, L. A.; Phys. Rev. B 2019, 99, 085117] allowing one to construct the correlation energy functionals by interpolation of the high and low-density limits for the given semilocal approximation. The current study extends the ACSC method to the meta-generalized gradient approximations (meta-GGA) level of theory, providing some new insights in this context. As an example, we construct the correlation energy functional on the basis of the high- and low-density limits of the Tao-Perdew-Staroverov-Scuseria (TPSS) functional. Arose in this way, the TPSS-ACSC functional is one-electron self-interaction free and accurate for the strictly correlated and quasi-two-dimensional regimes. Based on simple examples, we show the advantages and disadvantages of ACSC semilocal functionals and provide some new guidelines for future developments in this context.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
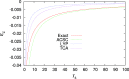
 , for the uniform electron gas. See the
text for details of the methods and exact reference curve.
, for the uniform electron gas. See the
text for details of the methods and exact reference curve.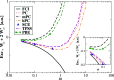
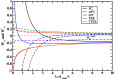

 .
.

References
-
- Kohn W.; Sham L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133.10.1103/PhysRev.140.A1133. - DOI
-
- Hohenberg P.; Kohn W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864.10.1103/PhysRev.136.B864. - DOI
-
- Levy M. On the simple constrained-search reformulation of the Hohenberg–Kohn theorem to include degeneracies and more (1964–1979). Int. J. Quantum Chem. 2010, 110, 3140–3144. 10.1002/qua.22895. - DOI
-
- Levy M. Mathematical thoughts in DFT. Int. J. Quantum Chem. 2016, 116, 802–804. 10.1002/qua.25133. - DOI
LinkOut - more resources
Full Text Sources
Research Materials

