Microscopic defect dynamics during a brittle-to-ductile transition
- PMID: 37812718
- PMCID: PMC10589702
- DOI: 10.1073/pnas.2305667120
Microscopic defect dynamics during a brittle-to-ductile transition
Abstract
Deformation of all materials necessitates the collective propagation of various microscopic defects. On Earth, fracturing gives way to crystal-plastic deformation with increasing depth resulting in a "brittle-to-ductile" transition (BDT) region that is key for estimating the integrated strength of tectonic plates, constraining the earthquake cycle, and utilizing deep geothermal resources. Here, we show that the crossing of a BDT in marble during deformation experiments in the laboratory is accompanied by systematic increase in the frequency of acoustic emissions suggesting a profound change in the mean size and propagation velocity of the active defects. We further identify dominant classes of emitted waveforms using unsupervised learning methods and show that their relative activity systematically changes as the rocks cross the brittle-ductile transition. As pressure increases, long-period signals are suppressed and short-period signals become dominant. At higher pressures, signals frequently come in avalanche-like patterns. We propose that these classes of waveforms correlate with individual dominant defect types. Complex mixed-mode events indicate that interactions between the defects are common over the whole pressure range, in agreement with postmortem microstructural observations. Our measurements provide unique, real-time data of microscale dynamics over a broad range of pressures (10 to 200 MPa) and can inform micromechanical models for semi-brittle deformation.
Keywords: brittle–ductile transitions; defect dynamics; rock deformation; ultrasound probes.
Conflict of interest statement
The authors declare no competing interest.
Figures
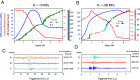

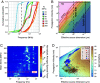

Comment in
-
A tale of two transitions: Linking the brittle-ductile transition to changing microphysical processes.Proc Natl Acad Sci U S A. 2023 Nov 28;120(48):e2316663120. doi: 10.1073/pnas.2316663120. Epub 2023 Nov 15. Proc Natl Acad Sci U S A. 2023. PMID: 37967210 Free PMC article. No abstract available.
References
-
- Kohlstedt D. L., Evans B., Mackwell S. J., Strength of the lithosphere: Constraints imposed by laboratory experiments. J. Geophys. Res. 100, 517–587 (1995).
-
- Bürgmann R., Dresen G., Rheology of the lower crust and upper mantle: Evidence from rock mechanics, geodesy, and field observations. Annu. Rev. Earth Planet. Sci. 36, 531–567 (2008).
-
- Evans B., Fredrich J. T., Wong T., “The brittle-ductile transition in rocks: Recent experimental and theoretical progress” in The Brittle-Ductile Transition in Rocks, Duba A. G., Durham W. B., Handin J. W., Wang H. F., Eds. (Geophysical Monograph Series, American Geophysical Union, Washington, DC, 1990), pp. 1–20.
-
- Pec M., Stünitz H., Heilbronner R., Drury M., Semi-brittle flow of granitoid fault rocks in experiments. J. Geophys. Res. Solid Earth 121, 1677–1705 (2016).
-
- Rutter E. H., On the nomenclature of mode of failure transitions in rocks. Tectonophysics 122, 381–387 (1986).
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

