Synchronizing chaos using reservoir computing
- PMID: 37832520
- PMCID: PMC10576628
- DOI: 10.1063/5.0161076
Synchronizing chaos using reservoir computing
Abstract
We attempt to achieve complete synchronization between a drive system unidirectionally coupled with a response system, under the assumption that limited knowledge on the states of the drive is available at the response. Machine-learning techniques have been previously implemented to estimate the states of a dynamical system from limited measurements. We consider situations in which knowledge of the non-measurable states of the drive system is needed in order for the response system to synchronize with the drive. We use a reservoir computer to estimate the non-measurable states of the drive system from its measured states and then employ these measured states to achieve complete synchronization of the response system with the drive.
© 2023 Author(s). Published under an exclusive license by AIP Publishing.
Conflict of interest statement
The authors have no conflicts to disclose.
Figures





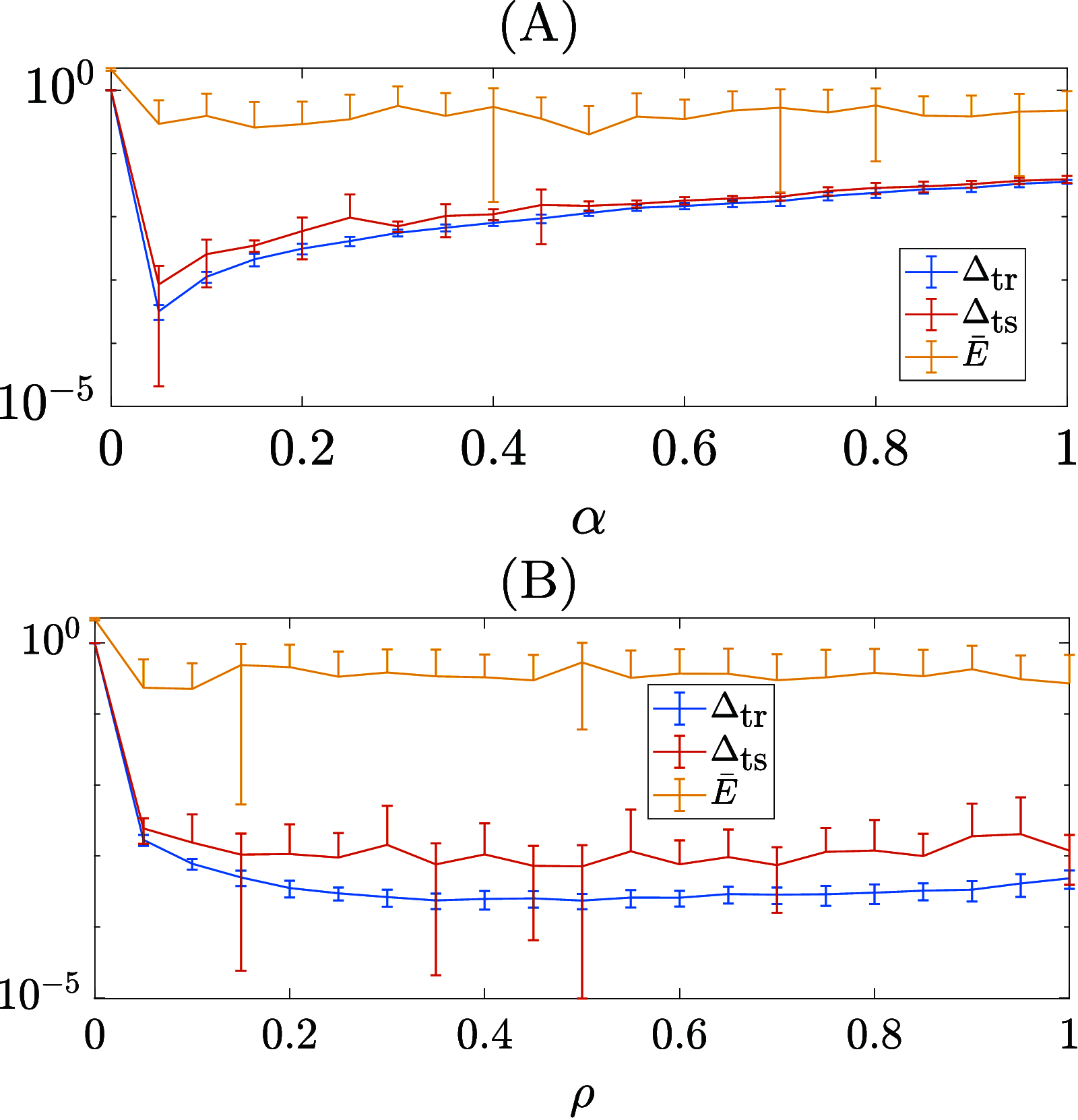


References
-
- Aranson I. and Rul’kov N., “Nontrivial structure of synchronization zones in multidimensional systems,” Phys. Lett. A 139(8), 375–378 (1989). 10.1016/0375-9601(89)90581-1 - DOI
-
- Pikovskii A. S., “Synchronization and stochastization of array of self-excited oscillators by external noise,” Radiophys. Quantum Electron. 27(5), 390–395 (1984). 10.1007/BF01044784 - DOI
-
- Fujisaka H. and Yamada T., “Stability theory of synchronized motion in coupled-oscillator systems,” Prog. Theor. Phys. 69(1), 32–47 (1983). 10.1143/PTP.69.32 - DOI
-
- Afraimovich V. S., Verichev N. N., and Rabinovich M. I., “Stochastic synchronization of oscillations in dissipative systems,” Radiophys. Quantum Electron. 29, 795–803 (1986).10.1007/BF01034476 - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

