Modeling the Impact of Agricultural Mitigation Measures on the Spread of Sharka Disease in Sweet Cherry Orchards

Abstract

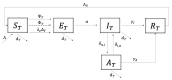
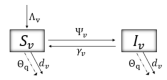
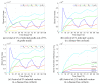
Sharka is a disease affecting stone fruit trees. It is caused by the Plum pox virus (PPV), with Myzus persicae being one of the most efficient aphid species in transmitting it within and among Prunus orchards. Other agricultural management strategies are also responsible for the spread of disease among trees, such as grafting and pruning. We present a mathematical model of impulsive differential equations to represent the dynamics of Sharka disease in the tree and vector population. We consider three transmission routes: grafting, pruning, and through aphid vectors. Grafting, pruning, and vector control occur as pulses at specific instants. Within the model, human risk perception towards disease influences these agricultural management strategies. Model results show that grafting with infected biological material has a significant impact on the spread of the disease. In addition, detecting infectious symptomatic and asymptomatic trees in the short term is critical to reduce disease spread. Furthermore, vector control to prevent aphid movement between trees is crucial for disease mitigation, as well as implementing awareness campaigns for Sharka disease in agricultural communities that provide a long-term impact on responsible pruning, grafting, and vector control.

Keywords: agricultural management; aphids; mathematical modeling; plum pox virus.

Figure 1

Schematics of the disease dynamics for trees. Table 1 and Table 2 describe, respectively, the variables and parameters used.

Figure 2

Schematics of the disease dynamics for vectors. Table 1 and Table 2 describe, respectively, the variables and parameters used.

Figure 3

Effects of grafting with infected material and arrival of infectious vectors on disease progress. (a–c) show the curves representing exposed trees ($E_T$, blue), symptomatic infectious trees ($I_T$, red), asymptomatic infectious trees ($A_T$, green), removed trees ($R_T$, yellow), and the total number of infectious trees ($I_T+A_T$, light blue), for four scenarios: (a) infection is only produced by inserting 1% of infected grafts out of $5\%$ of grafts made initially ($t_i=0$); (b,c) infection is only produced by the initial arrival of a percentage of infected vectors ($I_v\left(0\right)$) and no grafting with infected material occurs (${\mathrm{\Delta }}_T=0$). Initial conditions were taken: in (a) $S_T\left(0\right)=1$, $E_T\left(0\right)=I_T\left(0\right)=A_T\left(0\right)=R_T\left(0\right)=0$; $S_v\left(0\right)=1$, $I_v\left(0\right)=0$, $P\left(0\right)=P^{\ast }$; in (b) $S_v\left(0\right)=0.99$, $I_v\left(0\right)=0.01$ and the remaining as in (a); in (c) $S_v\left(0\right)=0.95$, $I_v\left(0\right)=0.05$ and the remaining as in (a). (d) shows the total number of infectious trees ($I_T+A_T$) for different initial numbers of infectious vectors ($I_v\left(0\right)$), under the same conditions as in (b,c). All other parameters used in the simulations are as in Table 2.

Figure 4

Effects of vector mobility on disease progress. (a–c) show the curves representing exposed trees ($E_T$, blue), infectious symptomatic trees ($I_T$, red), infectious asymptomatic trees ($A_T$, green), removed trees ($R_T$, yellow), and the total number of infectious trees ($I_T+A_T$, light blue) with respect to time, for $r=1$, $r=2$, and $r=3$, respectively. (d) shows the total number of infectious trees ($I_T+A_T$) with respect to time and for $r=1$ (blue), $r=2$ (black), and $r=3$ (red). The initial conditions were taken as in Figure 3a and all other parameters not specified here and used in the simulations are as in Table 2.

Figure 5

Effects of detection and removal of infected trees on disease progress. (a–c) show the curves representing exposed trees ($E_T$, blue), infectious symptomatic trees ($I_T$, red), infectious asymptomatic trees ($A_T$, green), removed trees ($R_T$, yellow), and the total number of infectious trees ($I_T+A_T$, light blue) with respect to time. (a,b) represent scenarios where only symptomatic trees ($I_T$) were removed after two years and one year on average, respectively, after presenting symptoms ($1/{\gamma }_T=720$ and $1/{\gamma }_T=360$, respectively). (c) represents a scenario in which symptomatic and asymptomatic trees were removed after an average of one year after becoming infectious ($1/{\gamma }_T=360$ and $1/{\gamma }_A=360$, respectively). (d) shows scenarios (a–c) for the total number of infectious trees ($I_T+A_T$). The initial conditions were taken as in Figure 3a and all other parameters not specified here and used in the simulations are as in Table 2.

Figure 6

Effects of risk perception on disease progress. (a–c) show the curve of the total number of infectious trees ($I_T+A_T$) with respect to time. (a) pictures three scenarios for different values of the resistance to change parameter, ${\lambda }_1$, and the rate of reaction to disease, ${\lambda }_2$, from Equation (3), where the black curve represents the smallest level of risk perception, and the red curve the largest. (b) shows three scenarios for a varying factor of increase in the risk perception, $\mu$, at instants $t_n$ (see Equation (5)), such that the black curve represents the lowest and the red curve the highest effectiveness of awareness campaigns. (c) shows scenarios (a,b) combined. The initial conditions were taken as in Figure 3a, and all other parameters not specified here and used in the simulations are in Table 2.