Dynamic analysis and control of a rice-pest system under transcritical bifurcations
- PMID: 37842048
- PMCID: PMC10573297
- DOI: 10.7717/peerj.16083
Dynamic analysis and control of a rice-pest system under transcritical bifurcations
Abstract
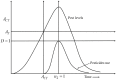
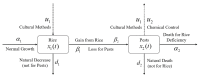
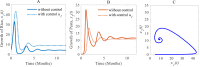
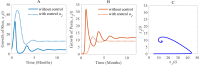
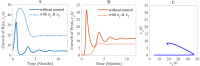
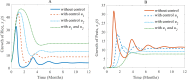
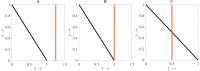
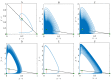
A decision model is developed by adopting two control techniques, combining cultural methods and pesticides in a hybrid approach. To control the adverse effects in the long term and to be able to evaluate the extensive use of pesticides on the environment and nearby ecosystems, the novel decision model assumes the use of pesticides only in an emergency situation. We, therefore, formulate a rice-pest-control model by rigorously modelling a rice-pest system and including the decision model and control techniques. The model is then extended to become an optimal control system with an objective function that minimizes the annual losses of rice by controlling insect pest infestations and simultaneously reduce the adverse impacts of pesticides on the environment and nearby ecosystems. This rice-pest-control model is verified by analysis, obtains the necessary conditions for optimality, and confirms our main results numerically. The rice-pest system is verified by stability analysis at equilibrium points and shows transcritical bifurcations indicative of acceptable thresholds for insect pests to demonstrate the pest control strategy.
Keywords: Decision model; Integrated pest management; Lotka-Volterra model; Nonlinear dynamics; Optimal control; Predator-prey.
©2023 Mandal et al.
Conflict of interest statement
The authors declare there are no competing interests.
Figures



Similar articles
-
Optimization of an integrated feedback control for a pest management predator-prey model.Math Biosci Eng. 2019 Sep 2;16(6):7963-7981. doi: 10.3934/mbe.2019401. Math Biosci Eng. 2019. PMID: 31698650
-
Pest management of a prey-predator model with sexual favoritism.Math Med Biol. 2009 Jun;26(2):97-115. doi: 10.1093/imammb/dqn025. Epub 2008 Nov 17. Math Med Biol. 2009. PMID: 19015368
-
A modelling methodology to assess the effect of insect pest control on agro-ecosystems.Sci Rep. 2015 Apr 23;5:9727. doi: 10.1038/srep09727. Sci Rep. 2015. PMID: 25906199 Free PMC article.
-
Ecology and management of arthropod pests of poultry.Annu Rev Entomol. 1990;35:101-26. doi: 10.1146/annurev.en.35.010190.000533. Annu Rev Entomol. 1990. PMID: 2405769 Review.
-
Considerations for Insect Learning in Integrated Pest Management.J Insect Sci. 2019 Jul 1;19(4):6. doi: 10.1093/jisesa/iez064. J Insect Sci. 2019. PMID: 31313814 Free PMC article. Review.
References
-
- Banerjee M, Petrovskii S. Self-organised spatial patterns and chaos in a ratio-dependent predator—prey system. Theoretical Ecology. 2011;4(1):37–53. doi: 10.1007/s12080-010-0073-1. - DOI
-
- Bazykin AD. Structural and dynamic stability of model predator-prey systems. International Institute for Applied Systems Analysis (IIASA) Research Memorandum; Laxenburg, Austria: 1976.
-
- Benett J, Bentur JC, Pasula IC, Krishnaiah K. New approaches to gall midge resistance in rice. New Delhi: International Rice Research Institute and Indian Council of Agricultural Research; 2004.
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Medical

