An Application of Spatio-temporal Modeling to Finite Population Abundance Prediction
- PMID: 37844016
- PMCID: PMC10569113
- DOI: 10.1007/s13253-023-00565-y
An Application of Spatio-temporal Modeling to Finite Population Abundance Prediction
Abstract
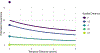
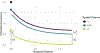
Spatio-temporal models can be used to analyze data collected at various spatial locations throughout multiple time points. However, even with a finite number of spatial locations, there may be a lack of resources to collect data from every spatial location at every time point. We develop a spatio-temporal finite-population block kriging (ST-FPBK) method to predict a quantity of interest, such as a mean or total, across a finite number of spatial locations. This ST-FPBK predictor incorporates an appropriate variance reduction for sampling from a finite population. Through an application to moose surveys in the east-central region of Alaska, we show that the predictor has a substantially smaller standard error compared to a predictor from the purely spatial model that is currently used to analyze moose surveys in the region. We also show how the model can be used to forecast a prediction for abundance in a time point for which spatial locations have not yet been surveyed. A separate simulation study shows that the spatio-temporal predictor is unbiased and that prediction intervals from the ST-FPBK predictor attain appropriate coverage. For ecological monitoring surveys completed with some regularity through time, use of ST-FPBK could improve precision. We also give an R package that ecologists and resource managers could use to incorporate data from past surveys in predicting a quantity from a current survey.
Keywords: forecast; kriging; resource monitoring; spatial; temporal; total.
Conflict of interest statement
Conflicts of Interest The authors declare no conflict of interest.
Figures

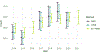

References
-
- Adde Antoine, Darveau Marcel, Barker Nicole, and Cumming Steven. 2020. “Predicting Spatiotemporal Abundance of Breeding Waterfowl Across Canada: A Bayesian Hierarchical Modelling Approach.” Diversity and Distributions 26 (10): 1248–63.
-
- Boertje Rodney D, Keech Mark A, Young Donald D, Kellie Kalin A, and Seaton C Tom. 2009. “Managing for Elevated Yield of Moose in Interior Alaska.” The Journal of Wildlife Management 73 (3): 314–27.
-
- Breivik Olav Nikolai, Aanes Fredrik, Søvik Guldborg, Aglen Asgeir, Mehl Sigbjørn, and Johnsen Espen. 2021. “Predicting Abundance Indices in Areas Without Coverage with a Latent Spatio-Temporal Gaussian Model.” ICES Journal of Marine Science 78 (6): 2031–42.
-
- Brus Dick J. 2021. “Statistical Approaches for Spatial Sample Survey: Persistent Misconceptions and New Developments.” European Journal of Soil Science 72 (2): 686–703.
-
- Chen Wanfang, Genton Marc G, and Sun Ying. 2021. “Space-Time Covariance Structures and Models.” Annual Review of Statistics and Its Application 8: 191–215.
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
