Establishing brain states in neuroimaging data

Abstract

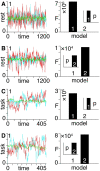
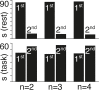
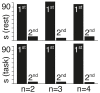
The definition of a brain state remains elusive, with varying interpretations across different sub-fields of neuroscience-from the level of wakefulness in anaesthesia, to activity of individual neurons, voltage in EEG, and blood flow in fMRI. This lack of consensus presents a significant challenge to the development of accurate models of neural dynamics. However, at the foundation of dynamical systems theory lies a definition of what constitutes the 'state' of a system-i.e., a specification of the system's future. Here, we propose to adopt this definition to establish brain states in neuroimaging timeseries by applying Dynamic Causal Modelling (DCM) to low-dimensional embedding of resting and task condition fMRI data. We find that ~90% of subjects in resting conditions are better described by first-order models, whereas ~55% of subjects in task conditions are better described by second-order models. Our work calls into question the status quo of using first-order equations almost exclusively within computational neuroscience and provides a new way of establishing brain states, as well as their associated phase space representations, in neuroimaging datasets.

Fig 1. The state of a three-node system in which the regions are coupled only to themselves (i.e., not to one another), as indicated by the looped grey arrows.

Each region is acted upon by a driving input, as indicated by the dashed central grey arrows. The future of the system is determined by its own present.

Fig 2. Same as Fig 1, except the state of the system (and hence its future) now depends upon its past as well as its present.

Fig 3

A) Left: first-order synthetic timeseries with normalized dependent variable (x). Right: Approximate log model evidence (variational free energy, ’F’) and associated probabilities (’p’, inset) following Bayesian model inversion, demonstrating that this timeseries is correctly associated with a first-order model. B) Same as A), except the timeseries on the left is second-order, as identified by the associated model comparison on the right.

Fig 4

Left: gradient-based timeseries with normalized dependent variables for single subjects. Right: approximate log model evidence (variational free energy, ’F’) and associated probabilities (’p’, inset) for first and second-order dynamics following Bayesian model inversion. A) An example of rest condition better described by a first-order model. B) An example of rest condition better described by a second-order model. C) An example of task condition better described by a first-order model. D) An example of task condition better described by a second-order model.

Fig 5

The proportion of subjects (s) that are better described by 1^st and 2^nd order models in rest (top) and task (bottom) conditions for n = 2, n = 3, and n = 4 gradients.

Fig 6

The proportion of subjects (s) that are better described by 1^st and 2^nd order models in rest (top) and task (bottom) conditions for n = 2, n = 3, and n = 4 gradients, for circularly shifted timeseries.

Fig 7

Temporal autocorrelation (y-axis) as a function of the lag (x-axis) for rest (left column) and task (right column) for n = 2 (first row), n = 3 (middle row) and n = 4 (bottom row) gradients. The results show that the subjects that are better described by second-order models (red) have consistently higher auto-correlations than the subjects that are better described by first-order models (blue).