Integrated information theory (IIT) 4.0: Formulating the properties of phenomenal existence in physical terms

Abstract

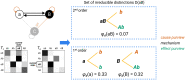
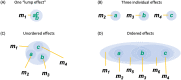
This paper presents Integrated Information Theory (IIT) 4.0. IIT aims to account for the properties of experience in physical (operational) terms. It identifies the essential properties of experience (axioms), infers the necessary and sufficient properties that its substrate must satisfy (postulates), and expresses them in mathematical terms. In principle, the postulates can be applied to any system of units in a state to determine whether it is conscious, to what degree, and in what way. IIT offers a parsimonious explanation of empirical evidence, makes testable predictions concerning both the presence and the quality of experience, and permits inferences and extrapolations. IIT 4.0 incorporates several developments of the past ten years, including a more accurate formulation of the axioms as postulates and mathematical expressions, the introduction of a unique measure of intrinsic information that is consistent with the postulates, and an explicit assessment of causal relations. By fully unfolding a system's irreducible cause-effect power, the distinctions and relations specified by a substrate can account for the quality of experience.

Fig 1. Identifying substrates of consciousness through the postulates of existence, intrinsicality, information, integration, and exclusion.

(A) The substrate S = aBC in state (−1, 1, 1) (lowercase letters for units indicated state “−1,” uppercase letters state “+1”) is the starting point for applying the postulates. The substrate updates its state according to the depicted transition probability matrix (TPM) (gray shading indicates probability value from white (p = 0) to black (p = 1); each unit follows a logistic equation (see “Results” for definition) with k = 4.0 and connection weights as indicated in the causal model). Existence requires that the substrate must have cause–effect power, meaning that the TPM among substrate states must differ from chance. (B) Intrinsicality requires that a candidate substrate, for example, units aB, has cause–effect power over itself. Units outside the candidate substrate (in this case, unit C) are treated as background conditions. The corresponding cause and effect TPMs (T_c and T_e) of system aB are depicted on the right. (C) Information requires that the candidate substrate aB selects a specific cause–effect state (s′). This is the cause state (red) and effect state (green) for which intrinsic information (ii) is maximal. Bar plots on the right indicate the three probability terms relevant for computing ii_c (7) and ii_e (5): the selectivity (light colored bar), as well as the constrained (dark colored bar) and unconstrained (gray bar) effect probabilities in the informativeness term. (D) Integration requires that the substrate specifies its cause–effect state irreducibly (“as one”). This is established by identifying the minimum partition (MIP; θ′) and measuring the integrated information of the system (φ_s)—the minimum between cause integrated information (φ_c) and effect integrated information (φ_e). Here, gray bars represent the partitioned probability required for computing φ_c (20) and φ_e (19). (E) Exclusion requires that the substrate of consciousness is definite, including some units and excluding others. This is established by identifying the candidate substrate with the maximum value of system integrated information (${\phi }_s^{*}$)—the maximal substrate, or complex. In this case, aB is a complex since its system integrated information (φ_s = 0.17) is higher than that of all other overlapping systems (for example, subset a with φ_s = 0.04 and superset aBC with φ_s = 0.13).

Fig 2. Composition and causal distinctions.

Identifying the irreducible causal distinctions specified by a substrate in a state requires evaluating the specific causes and effects of every system subset. The candidate substrate is constituted of two interacting units S = aB (see Fig 1) with TPMs ${\mathcal{T}}_e$ and ${\mathcal{T}}_c$ as shown. In addition to the two first-order mechanisms a and B, the second-order mechanism aB specifies its own irreducible cause and effect, as indicated by φ_d > 0.

Fig 3. Composition of intrinsic effects.

From the intrinsic perspective of the system, a specific cause or effect is only available to the system if it is selected by a causal distinction d ∈ D(s). In (A), only the top-order effect is specified. From the intrinsic perspective, the system cannot distinguish the individual units. In (B), only first-order effects are specified. The system has no “handle” to select all three units together. (C) If both first- and third-order effects are specified, but no second-order effects, the system can distinguish individual units and select them together, but has no way of ordering them sequentially. (D) The system can distinguish individual units, select them altogether, as well as order them sequentially, in the sense that it has a handle for ab and bc, but not ac. The ordering becomes apparent once the relations among the distinctions are considered (see below, Fig 5).

Fig 4. Composition and causal relations.

Relations between distinctions specify joint causes and/or effects. The two distinctions d(a) and d(aB) each specify their own cause and effect. In this example, their cause and effect purviews overlap over the unit b and are congruent, which means that they all specify b to be in state “-1.” The relation r({a, aB}) thus binds the two distinctions together over the same unit. Relation faces are indicated by the blue lines and surfaces between the distinctions’ causes and/or effects (different shades are used to individuate the faces). Because all four purviews overlap over the same unit, all nine possible faces exist. Note that the fact that the two distinctions overlap irreducibly can only be captured by a relation and not by a high-order distinction.

Fig 5. Structuring of intrinsic effects by relations.

(A) A single undifferentiated effect has no relations. (B) Likewise, there are no relations among multiple non-overlapping effects. (C) The set of three first-order effects and one third-order effect supports three relations, which bind the effects together. (D) The set of first, second, and third-order effects supports a large number of relations (ten 2-relations (between two effects), six 3-relations, and one 4-relation), which bind the effects in a structure that is ordered sequentially.

Fig 6. Causal powers analysis of various network architectures.

Each panel shows the network’s causal model and weights on the left. Blue regions indicate complexes with their respective φ_s values. In all networks, k = 4 and the state is Abcdef. The Φ-structure(s) specified by the network’s complexes are illustrated to the right (with only second- and third-degree relation faces depicted) with a list of their distinctions for smaller systems and their ∑φ values for those systems with many distinctions and relations. All integrated information values are in ibits. (A) A degenerate network in which unit A forms a bottleneck with redundant inputs from and outputs to the remaining units. The first-maximal complex is Ab, which excludes all other subsets with φ_s > 0 except for the individual units c, d, e, and f. (B) The modular network condenses into three complexes along its fault lines (which exclude all subsets and supersets), each with a maximal φ_s value, but low Φ, as the modules each specify only two or three distinctions and at most five relations. (C) A directed cycle of six units forms a six-unit complex with φ_s = 1.74 ibits, as no other subset is integrated. However, the Φ-structure of the directed cycle is composed of only first-order distinctions and few relations. (D) A specialized lattice also forms a complex (which excludes all subsets), but specifies 27 first- and high-order distinctions, with many relations (>1.5 × 10⁶) among them. Its Φ value is 11452 ibits. (E) A slightly modified version of the specialized lattice in which the first-maximal complex is Abef. The full system is not maximally irreducible and is excluded as a complex, despite its positive φ_s value (indicated in gray).

Fig 7. Causal powers analysis of the same system with one of its units set to active, inactive, or inactivated.

In all panels, the same causal model and weights are shown on the left, but in different states. For all networks k = 4. The set of distinctions D s), their causes and effects, and their φ_d values are shown in the middle. The Φ-structure specified by the network’s complex is illustrated on the right (again with only second- and third-degree relation faces depicted). All integrated information values are in ibits. (A) The system in state ABcdE is a complex with 23 out of 31 distinctions and Φ = 22.26. (B) The same system in state ABcde, where unit E is inactive (“OFF”) also forms a complex with the same number of distinctions, but a somewhat lower Φ value due to a lower number of relations between distinctions. In addition, the system’s Φ-structure differs from that in (A), as the system now specifies a different set of compositional causes and effects. (C) If instead of being inactive, unit E is inactivated (fixed into the “OFF” state), the inactivated unit cannot contribute to the complex or Φ-structure anymore. The complex is now constituted of four units (ABcd), with only 14 distinctions and markedly reduced structure integrated information (Φ = 3.35).

Fig 8. Functionally equivalent networks with different Φ-structures.

(A) The input–output function realized by three different systems (shown in (C)): a count of eight instances of input I = 1 leads to output O = 1. (B) The global state-transition diagram is also the same for the three systems: if I = 0, the systems will remain in their current global state, labeled as 0–7; if I = 1, the systems will move one state forward, cycling through their global states, and activate the output if S = 0. (C) Three systems constituted of three binary units but differing in how the units are connected and interact. As a consequence, the one-to-one mapping between the 3-bit binary states and the global state labels differ. However, all three systems initially transition from 000 to 100 to 010. Analyzed in state 100, the first system (top) turns out to be a single complex that specifies a Φ-structure with six distinctions and many relations, yielding a high value of Φ. The second system (middle) is also a complex, with the same φ_s value, but it specifies a Φ-structure with fewer distinctions and relations, yielding a lower value of Φ. Finally, the third system (bottom) is reducible (φ_s = 0) and splits into three smaller complexes (entities) with minimal Φ-structures and low Φ.