Mathematical solutions in internal dose assessment: A comparison of Python-based differential equation solvers in biokinetic modeling

Abstract

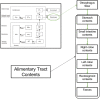
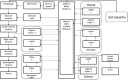
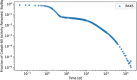
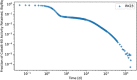
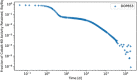
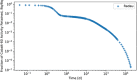
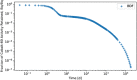
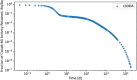
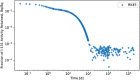
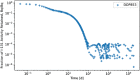
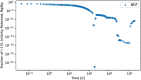
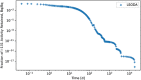
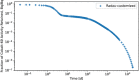
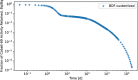
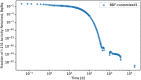
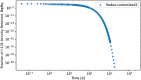
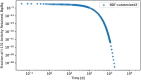
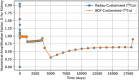
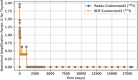
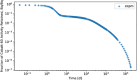
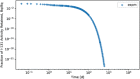
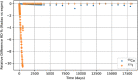
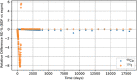
In biokinetic modeling systems employed for radiation protection, biological retention and excretion have been modeled as a series of discretized compartments representing the organs and tissues of the human body. Fractional retention and excretion in these organ and tissue systems have been mathematically governed by a series of coupled first-order ordinary differential equations (ODEs). The coupled ODE systems comprising the biokinetic models are usually stiff due to the severe difference between rapid and slow transfers between compartments. In this study, the capabilities of solving a complex coupled system of ODEs for biokinetic modeling were evaluated by comparing different Python programming language solvers and solving methods with the motivation of establishing a framework that enables multi-level analysis. The stability of the solvers was analyzed to select the best performers for solving the biokinetic problems. A Python-based linear algebraic method was also explored to examine how the numerical methods deviated from an analytical or semi-analytical method. Results demonstrated that customized implicit methods resulted in an enhanced stable solution for the inhaled⁶⁰Co (Type M) and¹³¹I (Type F) exposure scenarios for the inhalation pathway of the International Commission on Radiological Protection (ICRP) Publication 130 Human Respiratory Tract Model (HRTM). The customized implementation of the Python-based implicit solvers resulted in approximately consistent solutions with the Python-based matrix exponential method (expm). The differences generally observed between the implicit solvers andexpmare attributable to numerical precision and the order of numerical approximation of the numerical solvers. This study provides the first analysis of a list of Python ODE solvers and methods by comparing their usage for solving biokinetic models using the ICRP Publication 130 HRTM and provides a framework for the selection of the most appropriate ODE solvers and methods in Python language to implement for modeling the distribution of internal radioactivity.

Keywords: ODE solvers; Python; biokinetic modeling; compartmental analysis; internal dosimetry.

Figure 1.

Coupled inhalation compartmental model for cobalt (green arrow showing transfer from HRTM–oesophagus slow (Oes S) to the alimentary tract contents) (ICRP 2006, 2015). The subsequent dissolution into blood (systemic pool) from HRTM is indicated with the blue arrow, which is further distributed in organs and tissues in the rest of the body via a systemic model for cobalt (ICRP 2016a). The systemic model of cobalt was reproduced with permission from the ICRP Publication 134, figure 8.1 (ICRP 2016b).

Figure 2.

Transfer from HRTM to the alimentary tract contents for cobalt. From the ICRP Publication 100 (ICRP 2006), the human respiratory tract is connected to the digestion system through the slow component of the Oesophagus. The HRTM (top left) was reproduced with permission from the ICRP publication 130, figure 3.4 (ICRP 2015).

Figure 3.

Coupled Inhalation compartmental model for ¹³¹I (ICRP 2017). Arrows indicate a transfer of iodine from one organ/tissue to another with a designated transfer coefficient in units per day (d⁻¹). Similar to the model for cobalt, the respiratory tract is connected to the alimentary tract through the Oesophagus. The systemic model for iodine was reproduced with permission from the ICRP Publication 137, figure 5.2 (ICRP 2017).

Figure 4.

Retention for whole body computed for ⁶⁰Co Type M. The retention solution was obtained with the Python-based explicit Runge–Kutta method of order 5(4)–RK45. This yielded a diverging solution while computationally expensive for the biokinetic solving system and resulted in negative and oscillatory solutions over time.

Figure 5.

Retention for whole body computed for ⁶⁰Co Type M. The retention solution was obtained with the Python-based explicit Runge–Kutta method of order 3(2)–RK23. This method was computationally expensive for the biokinetic problem set and resulted in negative solutions.

Figure 6.

Retention for whole body computed for ⁶⁰Co Type M. The retention solution was obtained with the Python-based explicit Runge–Kutta method of order 8–DOP853. This method was computationally expensive for the biokinetic problem set and resulted in negative and oscillatory solutions.

Figure 7.

Retention for whole body computed for ⁶⁰Co Type M. The retention solution was obtained with the Python-based implicit Runge–Kutta method of the Radau IIA family of order 5. As a fast calculation for the biokinetic problem set employing default implementation, results yielded some negative solutions due to the large tolerances by defaults (negative solutions are not graphically visible but are present). This is not very evident on the plot but careful looked at the values in the output shows negative solution values.

Figure 8.

Retention for whole body computed for ⁶⁰Co Type M. The retention solution was obtained with the Python-based implicit multi-step variable-order (1–5) method. As a fast calculation for the biokinetic problem set, results yielded some negative solutions due to the large tolerances by defaults (negative solutions are not graphically visible but are present).

Figure 9.

Retention for whole body computed for ⁶⁰Co Type M. The retention solution was obtained with the Python-based adams/BDF method. As a fast calculation for the biokinetic problem set, results yielded negative and oscillatory values in some compartments giving a diverging solution.

Figure 10.

Whole body retention for ¹³¹I Type F. The retention solution was obtained with the Python-based explicit Runge–Kutta method of order 5(4)–RK45. This method was computationally expensive and resulted in significantly unstable solutions with significant oscillations after ∼ 90 d, where the solution diverges.

Figure 11.

Whole body retention for ¹³¹I Type F. The retention solution was obtained with the Python-based explicit Runge–Kutta method of order 3(2)—RK23. This method was computationally expensive for the biokinetic problem set and resulted in significantly unstable solutions with significant oscillations after ∼90 d, where the solution diverges.

Figure 12.

Whole body retention for ¹³¹I Type F. The retention solution was obtained with the Python-based explicit Runge–Kutta method of order 8–DOP853. This method was computationally expensive for the biokinetic problem set and resulted in significantly unstable solutions with significant oscillations over time, resulting in a diverging solution.

Figure 13.

Whole body retention for ¹³¹I Type F. The retention solution was obtained with the Python-based implicit Runge–Kutta method of the Radau IIA family of order 5. As a fast calculation for the biokinetic problem set, results yielded significantly unstable and oscillatory solutions. Default settings of the solver parameters were used for this case.

Figure 14.

Whole body retention for ¹³¹I Type F. The retention solution was obtained with the Python-based implicit multi-step variable-order (1–5) method. As a fast calculation for the biokinetic problem set, results yielded significantly unstable and oscillatory solutions. Default settings of the solver parameters were used for this case.

Figure 15.

Whole body retention for ¹³¹I Type F. The retention solution was obtained with the Python-based adams/BDF method. As a fast calculation for the biokinetic problem set, results yielded significantly unstable and oscillatory solutions.

Figure 16.

Whole body retention for ⁶⁰Co Type M. The retention solution was obtained with the Python-based solvers implicit Runge–Kutta method of the Radau IIA family of order 5. As a fast calculation for the biokinetic problem set, results yielded stable solutions. This solution depicts the instance of enhancing the local error control for Radau by reducing the relative and absolute tolerances.

Figure 17.

Whole body retention for ⁶⁰Co Type M. The retention solution was obtained with the Python-based implicit multi-step variable-order (1–5) method. As a fast calculation for the biokinetic problem set, results yielded few oscillations in a few compartments between outputting exactly 0 and values close to 0 (10⁻⁴⁵), which can essentially be considered zero. This solution depicts the instance of enhancing the local error control for BDF by reducing the relative and absolute tolerances.

Figure 18.

Whole body retention for ¹³¹I Type F. The retention solution was obtained with the Python-based implicit Runge–Kutta method of the Radau IIA family of order 5. As a fast calculation for the biokinetic problem set, results yielded significantly unstable solutions. This solution depicts the instance for enhancing the local error control for Radau by reducing the relative and absolute tolerances.

Figure 19.

Whole body retention for ¹³¹I Type F. The retention solution was obtained with the Python-based implicit multi-step variable-order (1–5) method. As a fast calculation for the biokinetic problem set, results yielded significantly unstable solutions. This solution depicts the instance for enhancing the local error control for BDF by reducing the relative and absolute tolerances.

Figure 20.

Whole body retention for ¹³¹I Type F. The retention solution was obtained with the Python-based Runge–Kutta method of the Radau IIA family of order 5. As a fast calculation for the biokinetic problem set, results yielded stable solutions. A stable solution was obtained by restricting the step size to a maximum of 0.2 in addition to local error control via relative and absolute tolerances.

Figure 21.

Whole body retention for ¹³¹I Type F. The retention solution was obtained with the Python-based implicit multi-step variable-order (1–5) method. As a fast calculation for the biokinetic problem set, results yielded stable solutions. A stable solution was obtained by restricting the step size to a maximum of 0.2 in addition to local error control via relative and absolute tolerances.

Figure 22.

Stability analysis of the Python-based solvers (Radau and BDF) using numerical amplification factor, G over 50-year time span for Kidney retention solutions of ⁶⁰Co.

Figure 23.

Stability analysis of the Python-based solvers (Radau and BDF) using numerical amplification factor, G over 50 year time span for computed activity retained in the Thyroid of ¹³¹I.

Figure 24.

Whole body retention computed using Python-based matrix exponential method for ⁶⁰Co Type M. The result depicts stable solutions with a fast calculation time of approximately 0.4 s.

Figure 25.

Whole body retention computed using Python-based matrix exponential method for ¹³¹I Type F. The result depicts stable solutions for the highly stiff system with a fast calculation time of approximately 0.4 s.

Figure 26.

The percent relative difference (RD %) for whole body retention solution between Python-based expm and Radau (Customized for ⁶⁰Co and Customized 2 for ¹³¹I) for a 50 year time period.

Figure 27.

The percent relative difference (RD %) for whole body retention solution between Python-based expm and BDF (Customized for ⁶⁰Co and Customized 2 for ¹³¹I) for a 50 year time period.