A Somatosensory Computation That Unifies Limbs and Tools

Abstract

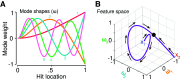
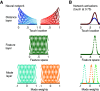
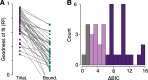
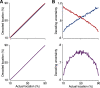
It is often claimed that tools are embodied by their user, but whether the brain actually repurposes its body-based computations to perform similar tasks with tools is not known. A fundamental computation for localizing touch on the body is trilateration. Here, the location of touch on a limb is computed by integrating estimates of the distance between sensory input and its boundaries (e.g., elbow and wrist of the forearm). As evidence of this computational mechanism, tactile localization on a limb is most precise near its boundaries and lowest in the middle. Here, we show that the brain repurposes trilateration to localize touch on a tool, despite large differences in initial sensory input compared with touch on the body. In a large sample of participants, we found that localizing touch on a tool produced the signature of trilateration, with highest precision close to the base and tip of the tool. A computational model of trilateration provided a good fit to the observed localization behavior. To further demonstrate the computational plausibility of repurposing trilateration, we implemented it in a three-layer neural network that was based on principles of probabilistic population coding. This network determined hit location in tool-centered coordinates by using a tool's unique pattern of vibrations when contacting an object. Simulations demonstrated the expected signature of trilateration, in line with the behavioral patterns. Our results have important implications for how trilateration may be implemented by somatosensory neural populations. We conclude that trilateration is likely a fundamental spatial computation that unifies limbs and tools.

Keywords: computation; embodiment; space; tactile localization; tool use.

Figure 1.

Model of trilateration and tool-sensing paradigm. A, The trilateral computation applied to the space of the arm (bottom) a hand-held rod (top). Distance estimates from sensory input (black) and each boundary (d1 and d2) are integrated (purple) to form a location estimate. B, In our model, the noise in each distance estimate (d1, d2) increases linearly with distance. The integrated estimate forms an inverted U-shaped pattern. C, Two tool-sensing tasks used to characterize tactile localization on a hand-held rod. The purple arrow corresponds to the location of touch in tool-centered space. The red square corresponds to the judgment of location within the computer screen.

Figure 2.

Vibration modes and feature space. A, The shape of the first five modes $\omega$ for contact on a cantilever rod. The weight of each mode varies as a function of hit location. Each hit location is characterized by a unique combination of mode weights. B, The vibration-location feature space (purple) from handle (X₁) to tip (X₂). This feature space is isomorphic with the actual physical space of the rod. $\omega$ corresponds to a resonant frequency, the black dot corresponds to the hit location (as in Fig. 1A) within the feature space, and the arrows are the gradients of distance estimation during trilateration.

Figure 3.

Neural network implementation of trilateration. A, Neural network implementation of trilateration: (lower panel) the Mode layer is composed of subpopulations (two shown here) sensitive to the weight of individual modes (Fig. 2A), which are location-dependent; (middle panel). Feature layer takes input from the mode layer and encodes the feature space (Fig. 2B), which forms the isomorphism with the physical space of the tool; (upper panel) the Distance layer is composed of two subpopulations of neurons with distance-dependent gradients in tuning properties (shown: firing rate and tuning width). The distance of a tuning curve from its “anchor” is coded by the luminance, with darker colors corresponding to neurons that are closer to the spatial boundary. B, Activations for each layer of the network averaged over 5000 simulations when touch was at 0.75 (space between 0 and 1). Each dot corresponds to a unit of the neural network. (lower panel) mode layer, with three of five subpopulations shown; (middle panel) feature layer; (upper panel) distance layer of localization for each decoding subpopulation.

Figure 4.

Localization and variable error for both tasks. A, Regressions fit to the localization judgments for both the image-based (blue) and space-based (orange) tasks. Error bars correspond to the group-level 95% confidence interval. B, Group-level variable errors for both tasks. Error bars correspond to the group-level 95% confidence interval.

Figure 5.

Trilateration model provides a good fit to localization behavior. A, Fit of the trilateration model to the group-level variable error (black dots). The purple line corresponds to the model fit. The light gray line and squares correspond to variable errors for localization on the arm observed in Miller et al. (2022); note that these data are size adjusted to account for differences in arm and rod size. B, Fit of the trilateration model to the variable errors of six randomly chosen participants. The fit of the trilateration model for each participant’s behavior can be seen in Extended Data Figures 5-1 and 5-2.

Figure 6.

Trilateration provides a better fit to the data than boundary truncation. A, Participant-level goodness of fits (R²) for the trilateration model (left, purple) and the boundary truncation model (right, green). For each participant, trilateration was a better fit to the data. B, Histogram of the ΔBIC values used to adjudicate between the two models, color-coded by the strength of the evidence in favor of trilateration. Purple corresponds to substantial evidence in favor of trilateration; pink corresponds to moderate evidence in favor of trilateration; gray corresponds to weak/equivocal evidence in favor of trilateration. Note that in no case did the boundary truncation model provide a better fit to the localization data (i.e., ΔBIC < 0).

Figure 7.

Neural network simulations. A, Localization accuracy for the estimates of each decoding subpopulation (upper panel; L₁, blue; L₂, red) and after integration by the Bayesian decoder (lower panel; L_INT, purple). B, Decoding noise for each decoding subpopulation (upper panel) increased as a function of distance from each landmark. Note that distance estimates are made from the 10% and 90% locations for the first (blue) and second (red) decoding subpopulations, respectively. Integration via the Bayesian decoder (lower panel) led to an inverted U-shaped pattern across the surface. Note the differences in the y-axis range for both panels. The results of decoding for the mode and feature space layers of the network can be seen in Extended Data Figure 7-1.

Figure 8.

Simulations of multisegmented rods. We simulated how trilateration operates within rods with different numbers of segments. Here, we show the predicted patterns of variability for (A) a single-segment rod (used in present study) and (B) two-segment (left) and three-segment (right) rods. The magnitude of variable error is color-coded as red-to-blue (low-to-high). The inverted U-shaped pattern of variability was observed in each segment.