Measurement-induced entanglement and teleportation on a noisy quantum processor

Abstract

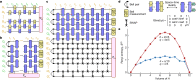
Measurement has a special role in quantum theory¹: by collapsing the wavefunction, it can enable phenomena such as teleportation² and thereby alter the 'arrow of time' that constrains unitary evolution. When integrated in many-body dynamics, measurements can lead to emergent patterns of quantum information in space-time^3-10 that go beyond the established paradigms for characterizing phases, either in or out of equilibrium^11-13. For present-day noisy intermediate-scale quantum (NISQ) processors¹⁴, the experimental realization of such physics can be problematic because of hardware limitations and the stochastic nature of quantum measurement. Here we address these experimental challenges and study measurement-induced quantum information phases on up to 70 superconducting qubits. By leveraging the interchangeability of space and time, we use a duality mapping^9,15-17 to avoid mid-circuit measurement and access different manifestations of the underlying phases, from entanglement scaling^3,4 to measurement-induced teleportation¹⁸. We obtain finite-sized signatures of a phase transition with a decoding protocol that correlates the experimental measurement with classical simulation data. The phases display remarkably different sensitivity to noise, and we use this disparity to turn an inherent hardware limitation into a useful diagnostic. Our work demonstrates an approach to realizing measurement-induced physics at scales that are at the limits of current NISQ processors.

Fig. 1. Monitored circuits and space–time duality mapping.

a, A random (1 + 1)-dimensional monitored quantum circuit composed of both unitary gates and measurements. b, An equivalent dual (1 + 1)-dimensional shallow circuit of size L_x × L_y and depth T with all measurements at the final time formed from a space–time duality mapping of the circuit in a. Because of the non-unitarity nature of measurements, there is freedom as to which dimensions are viewed as ‘time’ and which as ‘space’. In this example, L_y is set by the (1 + 1)D circuit depth and L_x by its spatial size, and T is set by the measurement rate. c, Classical post-processing on a computer of the measurement record (quantum trajectory), and quantum-state readout of a monitored circuit can be used to diagnose the underlying information structures in the system.

Fig. 2. Implementation of space–time duality in 1D.

a, A quantum circuit composed of non-unitary two-qubit operations in a brickwork pattern on a chain of 12 qubits with 7 time steps. Each two-qubit operation can be a combination of unitary operations and measurement. b, The space–time dual of the circuit shown in a with the roles of space and time interchanged. The 12-qubit wavefunction |Ψ_m⟩ is temporally extended along Q₇. c, In the experiment on a quantum processor, a set of 12 ancillary qubits $Q_1^{\prime }\dots Q_{12}^{\prime }$ and a network of SWAP gates are used to teleport |Ψ_m⟩ to the ancillary qubits. d, Illustration of the two-qubit gate composed of an fSim unitary and random Z rotations with its space–time dual, which is composed of a mixture of unitary and measurement operations. The power h of the Z rotation is random for every qubit and periodic with each cycle of the circuit. e, Second Renyi entropy as a function of the volume of a subsystem A from randomized measurements and post-selection on Q₁…Q₆. The data shown are noise mitigated by subtracting an entropy density matching the total system entropy. See the Supplementary Information for justification.

Fig. 3. 1D entanglement phases obtained from 2D shallow quantum circuits.

a, Schematic of the 2D grid of qubits. At each cycle (blue boxes) of the circuit, random single-qubit and two-qubit iSWAP-like gates are applied to each qubit in the cycle sequence shown. The random single-qubit gate (SQ, grey) is chosen randomly from the set $\left\{\sqrt{X^{\pm 1}},\sqrt{Y^{\pm 1}},\sqrt{W^{\pm 1}},\sqrt{V^{\pm 1}}\right\}$, where $W=\left(X+Y\right)/\sqrt{2}$ and $V=\left(X-Y\right)/\sqrt{2}$. At the end of the circuit, the lower M = 12 qubits are measured and post-selected on the most probable bitstring. b, Second Renyi entropy of contiguous subsystems A of the L = 7 edge qubits at various depths. The measurement is noise mitigated in the same way as in Fig. 2. c, Second Renyi mutual information ${\mathcal{I}}_{AB}^{\left(2\right)}$ between two-qubit subsystems A and B against depth T and distance x (the number of qubits between A and B). d, ${\mathcal{I}}_{AB}^{\left(2\right)}$ as a function of T for two-qubit subsystems A and B at maximum separation. e, ${\mathcal{I}}_{AB}^{\left(2\right)}$ versus x for T = 3 and T = 6 for different volumes of A and B.

Fig. 4. Decoding of local order parameter, measurement-induced teleportation and finite-size analysis.

a, Schematic of the processor geometry and decoding procedure. The gate sequence is the same as in Fig. 3 with depth T = 5. The decoding procedure involves classically computing the Bloch vector a_m of the probe qubit (pink) conditional on the experimental measurement record m (yellow). The order parameter ζ is calculated by means of the cross-correlation between the measured probe bit z_p and ${\tau }_m=\mathsf{s}\mathsf{i}\mathsf{g}\mathsf{n}({\mathbf{a}}_m\cdot \hat{z})$, which is +1 if a_m points above the equator of the Bloch sphere and −1 if it points below. b, Decoded order parameter ζ and error-mitigated order parameter $\tilde{\zeta }=\zeta /\zeta \left(r_{\max }\right)$ as a function of the decoding radius r for different N and ρ = 1. c, $\zeta \left(r_{\max }\right)$ as a function of the gate density ρ for different N. The inset shows that for small ρ, ζ(r_max) remains constant as a function of N (disentangling phase), whereas for larger ρ, ζ(r_max) decays exponentially with N, implying sensitivity to noise of arbitrarily distant qubits (entangling phase). d, Error-mitigated proxy entropy ${\tilde{S}}_{\mathrm{proxy}}$ as a function of the decoding radius for ρ = 0.3 (triangles) and ρ = 1 (circles). In the disentangling phase, ${\tilde{S}}_{\mathrm{proxy}}$ decays rapidly to 0, independent of the system size. In the entangling phase, ${\tilde{S}}_{\mathrm{proxy}}$ remains large and finite up to r_max − 1. e, ${\tilde{S}}_{\mathrm{proxy}}$ at N = 40 as a function of r for different ρ, revealing a crossover between the entangling and disentangling phases for intermediate ρ. f, ${\tilde{S}}_{\mathrm{proxy}}$ at r = r_max − 1 as a function of ρ for N = 12, 24, 40 and 58 qubits. The curves for different sizes approximately cross at ρ_c ≈ 0.9. Inset, schematic showing the decoding geometry for the experiment. The pink and grey lines encompass the past light cones (at depth T = 5) of the probe qubit and traced-out qubits at r = r_max − 1, respectively. Data were collected from 2,000 random circuit instances and 1,000 shots each for every value of N and ρ.