A parametric study on the analysis of thermosolutal convection for magneto-hydrodynamics dependent viscous fluid

Abstract

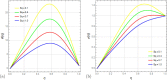
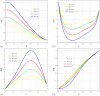
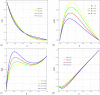
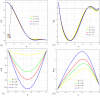
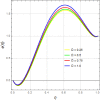
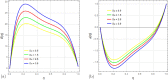
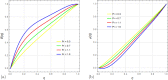
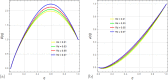
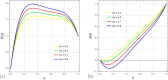
This article explores the influence of Joule heating and viscous dissipation on the unsteady three-dimensional squeezing flow of Newtonian fluid. The flow in a rotating channel with a lower stretched permeable wall is observed under the influence of a uniform magnetic field. The impact of thermal radiation is also considered. The effects of mass and heat transfer on the squeezing flow of Newtonian fluids are observed and modelled using the four fundamental governing equations of fluid flow: the mass equation, momentum equation, concentration equation, and energy equation. Using the appropriate similarity transformations, the resultant non-linear partial differential equations are then transformed into ordinary differential equations. The analytical strategy is developed using the homotopy analysis method to obtain the series solution. The influence of several physical parameters, including the squeezing parameter, the suction parameter, the magnetic number, the rotation parameter, the Eckert number, the Prandtl number, the Dufour number, the Soret number, the radiation parameter, and the Schmidt number, on the velocity profile, energy, and concentration are also discussed through graphs. Additionally, it is observed that enhancing the top plate's squeezing impact causes a rise in the velocity profile while lowering the temperature and concentration distribution. It is also found that for the velocity field, increasing the magnetic number shows a decrease in the value of the velocity field along the y- and z-axis, whereas the velocity field along the x-axis exhibits dual behavior, such that it initially falls as the magnetic number intensifies but starts to rise in the upper region of the channel. The impact of the Dufour, Soret, and Eckert numbers on temperature and concentration distribution is also studied. It is found that while these numbers directly affect the temperature distribution, the mass distribution follows the opposite trend. Also, it is noticed that the thermal radiation parameter is an increasing function of temperature and mass distribution. Further, graphs and tables are presented to illustrate an error analysis.

Figure 1

Geometry of the problem.

Figure 2

Error profile for $f(\eta )$, $g(\eta )$, $\theta (\eta )$, and $\varphi (\eta )$ with $S_q=1.0$, $\mathrm{\Omega }=2$, $D_u=0.2$, $P_r=0.1$, $S_c=0.1$, $S_r=1$, $S=0.5$, $M=0.5$, $R_d=1$, $E_c=0.2$, and $\delta =0.1$.

Figure 3

Three dimensional view of the profiles $f(\eta )$, $g(\eta )$, $\theta (\eta )$, and $\varphi (\eta )$ with $S_q=1.0$, $\mathrm{\Omega }=2$, $D_u=0.2$, $P_r=0.1$, $S_c=0.1$, $S_r=1$, $S=0.5$, $M=0.5$, $R_d=1$, $E_c=0.2$, and $\delta =0.1$.

Figure 4

Impact of squeezing number $S_q$ on velocity profiles $f^{\prime }(\eta )$ and $g(\eta )$ with $\mathrm{\Omega }=1$, $D_u=0.5$, $P_r=0.5$, $S_c=0.9$, $S_r=0.2$, $S=0.8$, $M=10$, $R_d=1$, $E_c=0.2$ and $\delta =0.1$.

Figure 5

Impact of squeezing number $S_q$ on $\theta (\eta )$ and $\varphi (\eta )$ with $\mathrm{\Omega }=1$, $D_u=0.5$, $P_r=0.5$, $S_c=0.9$, $S_r=0.2$, $S=0.8$, $M=10$, $R_d=1$, $E_c=0.2$ and $\delta =0.1$.

Figure 6

Impact of suction parameter S on profiles $f(\eta )$, $f^{\prime }(\eta )$, $\theta (\eta )$ and $\varphi (\eta )$ with $\mathrm{\Omega }=0.25$, $D_u=0.1$, $P_r=0.25$, $S_c=0.5$, $S_r=0.25$, $S_q=0.1$, $M=10$, $R_d=0.1$, $E_c=0.1$ and $\delta =0.1$.

Figure 7

Impact of magnetic number M on profiles $f^{\prime }(\eta )$, $g(\eta )$, $\theta (\eta )$ and $\varphi (\eta )$ with $\mathrm{\Omega }=1$, $D_u=1$, $P_r=2.5$, $S_c=0.5$, $S_r=0.5$, $S=1$, $S_q=2.5$, $R_d=0.1$, $E_c=1.5$ and $\delta =0.1$.

Figure 8

Impact of rotation parameter $\mathrm{\Omega }$ on profiles $f(\eta )$, $f^{\prime }(\eta )$, $g(\eta )$ and $\theta (\eta )$ with $S_q=0.1$, $D_u=0.1$, $P_r=0.1$, $S_c=0.1$, $S_r=0.02$, $S=2.5$, $M=15$, $R_d=0.1$, $E_c=0.1$ and $\delta =0.1$.

Figure 9

Impact of rotation parameter $\mathrm{\Omega }$ on concentration profile $\varphi (\eta )$ with $S_q=20$, $D_u=0.1$, $P_r=0.01$, $S_c=2.5$, $S_r=0.025$, $S=5$, $M=10$, $R_d=0.1$, $E_c=20$ and $\delta =0.1$.

Figure 10

Impact of Soret number $S_r$ on temperature profile $\theta (\eta )$ and concentration profile $\varphi (\eta )$ with $\mathrm{\Omega }=0.1$, $D_u=0.1$, $P_r=2$, $S_c=0.9$, $S_q=0.25$, $S=1$, $M=1.5$, $R_d=0.1$, $E_c=0.1$ and $\delta =0.1$.

Figure 11

Impact of Dufour number $D_u$ on temperature profile $\theta (\eta )$ and concentration profile $\varphi (\eta )$ with $\mathrm{\Omega }=0.1$, $S_q=0.5$, $P_r=2$, $S_c=0.25$, $S_r=0.4$, $S=2$, $M=0.5$, $R_d=0.1$, $E_c=2.5$ and $\delta =0.1$.

Figure 12

Impact of Prandtl number $P_r$ on temperature profile $\theta (\eta )$ and concentration profile $\varphi (\eta )$ with $\mathrm{\Omega }=1$, $D_u=0.5$, $S_q=0.5$, $S_c=0.5$, $S_r=1.5$, $S=0.5$, $M=0.5$, $R_d=0.5$, $E_c=0.5$ and $\delta =0.1$.

Figure 13

Impact of Eckert number $E_c$ on temperature profile $\theta (\eta )$ and concentration profile $\varphi (\eta )$ with $\mathrm{\Omega }=1$, $D_u=1$, $S_q=0.5$, $S_c=0.5$, $S_r=0.5$, $S=1$, $M=0.5$, $R_d=0.5$, $P_r=2.5$ and $\delta =0.1$.

Figure 14

Impact of Radiation parameter $R_d$ on temperature profile $\theta (\eta )$ and concentration profile $\varphi (\eta )$ with $\mathrm{\Omega }=0.5$, $D_u=0.5$, $S_q=0.5$, $S_c=0.5$, $S_r=0.5$, $S=1$, $M=5$, $P_r=0.5$, $E_c=0.5$ and $\delta =0.1$.

Figure 15

Impact of Schmidt number $S_c$ on temperature profile $\theta (\eta )$ and concentration profile $\varphi (\eta )$ with $\mathrm{\Omega }=1$, $D_u=1.5$, $S_q=0.5$, $R_d=0.5$, $S_r=0.5$, $S=1$, $M=0.5$, $P_r=2.5$, $E_c=0.5$ and $\delta =0.1$.