CONSISTENT SPECTRAL CLUSTERING OF NETWORK BLOCK MODELS UNDER LOCAL DIFFERENTIAL PRIVACY
- PMID: 37860129
- PMCID: PMC10586058
- DOI: 10.29012/jpc.811
CONSISTENT SPECTRAL CLUSTERING OF NETWORK BLOCK MODELS UNDER LOCAL DIFFERENTIAL PRIVACY
Abstract
The stochastic block model (SBM) and degree-corrected block model (DCBM) are network models often selected as the fundamental setting in which to analyze the theoretical properties of community detection methods. We consider the problem of spectral clustering of SBM and DCBM networks under a local form of edge differential privacy. Using a randomized response privacy mechanism called the edge-flip mechanism, we develop theoretical guarantees for differentially private community detection, demonstrating conditions under which this strong privacy guarantee can be upheld while achieving spectral clustering convergence rates that match the known rates without privacy. We prove the strongest theoretical results are achievable for dense networks (those with node degree linear in the number of nodes), while weak consistency is achievable under mild sparsity (node degree greater than ). We empirically demonstrate our results on a number of network examples.
Keywords: community detection; differential privacy; spectral clustering; stochastic block model.
Figures
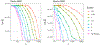
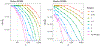


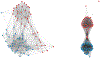

References
-
- Abbe E. Community detection and stochastic block models: Recent developments. Journal of Machine Learning Research, 18(177):1–86, 2018. http://jmlr.org/papers/v18/16-480.html.
-
- Abbe E, Fan J, and Wang K. An ℓp theory of PCA and spectral clustering, 2021. http://arxiv.org/abs/2006.14062.
-
- Adamic LA and Glance N. The political blogosphere and the 2004 US election: divided they blog. In Proceedings of the 3rd International Workshop on Link Discovery, pages 36–43, 2005. 10.1145/1134271.1134277. - DOI
-
- Athreya A, Priebe CE, Tang M, Lyzinski V, Marchette DJ, and Sussman DL. A limit theorem for scaled eigenvectors of random dot product graphs. Sankhya A, 78(1): 1–18, 2016. ISSN 0976–836X. 10.1007/s13171-015-0071-x. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources
