Activity-dependent glassy cell mechanics II: Nonthermal fluctuations under metabolic activity

Abstract

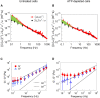
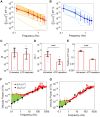
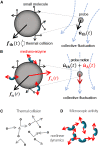
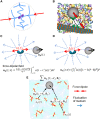
The glassy cytoplasm, crowded with bio-macromolecules, is fluidized in living cells by mechanical energy derived from metabolism. Characterizing the living cytoplasm as a nonequilibrium system is crucial in elucidating the intricate mechanism that relates cell mechanics to metabolic activities. In this study, we conducted active and passive microrheology in eukaryotic cells, and quantified nonthermal fluctuations by examining the violation of the fluctuation-dissipation theorem. The power spectral density of active force generation was estimated following the Langevin theory extended to nonequilibrium systems. However, experiments performed while regulating cellular metabolic activity showed that the nonthermal displacement fluctuation, rather than the active nonthermal force, is linked to metabolism. We discuss that mechano-enzymes in living cells do not act as microscopic objects. Instead, they generate meso-scale collective fluctuations with displacements controlled by enzymatic activity. The activity induces structural relaxations in glassy cytoplasm. Even though the autocorrelation of nonthermal fluctuations is lost at long timescales due to the structural relaxations, the nonthermal displacement fluctuation remains regulated by metabolic reactions. Our results therefore demonstrate that nonthermal fluctuations serve as a valuable indicator of a cell's metabolic activities, regardless of the presence or absence of structural relaxations.

Figure 1

Schematics of AMR, PMR, and FDT violation. (A) In AMR, a sinusoidal external force is applied to a probe particle using a drive laser (λ = 1064 nm). The probe particle’s displacement is measured using a probe laser (λ = 830 nm). Although the minute response to the applied force is hidden behind (non-) thermal fluctuations, a lock-in amplifier detects the phase delay $\theta ={\tau }_u\omega$ and amplitude of the response $\left|⟨\stackrel{⌢}{u}\left(\omega \right)⟩\right|$, yielding the response function α(ω) and viscoelasticity G(ω). (B) In passive MR, spontaneous probe fluctuations are measured using an 830-nm laser. By calculating the PSD of the fluctuation, the FDT ($⟨{\left|\tilde{u}\left(\omega \right)\right|}^2⟩=2k_{\mathrm{B}}T{\alpha }^{″}\left(\omega \right)/\omega$ in (C) and $⟨{\left|\tilde{\upsilon }\left(\omega \right)\right|}^2⟩=2\omega k_{\mathrm{B}}T{\alpha }^{″}\left(\omega \right)$ in (D)) is directly tested. In out-of-equilibrium systems where FDT is violated, the PSD of active fluctuations is obtained as $⟨{\left|{\tilde{u}}_{\mathrm{A}}\left(\omega \right)\right|}^2⟩=⟨{\left|\tilde{u}\left(\omega \right)\right|}^2⟩-2k_{\mathrm{B}}T{\alpha }^{″}\left(\omega \right)/\omega$ and $⟨{\left|{\tilde{\upsilon }}_{\mathrm{A}}\left(\omega \right)\right|}^2⟩=⟨{\left|\tilde{\upsilon }\left(\omega \right)\right|}^2⟩-2\omega k_{\mathrm{B}}T{\alpha }^{″}\left(\omega \right)$, respectively. To see this figure in color, go online.

Figure 2

Results of MR experiments in HeLa cells w and w/o ATP depletion. FDT violation in (A) untreated (n = 24) and (B) ATP-depleted HeLa cells (n = 7). The difference between $⟨{\left|\tilde{u}\left(\omega \right)\right|}^2⟩$ measured with PMR (red circles) and $⟨{\left|{\tilde{u}}_{\text{th}}\left(\omega \right)\right|}^2⟩=2k_{\mathrm{B}}T{\alpha }^{″}\left(\omega \right)/\omega$ measured with AMR (black circles), shown by the green-colored region at low frequencies, indicates nonthermal fluctuation $⟨{\left|{\tilde{u}}_{\mathrm{A}}\left(\omega \right)\right|}^2⟩$. The peaks at approximately 100 and 20 Hz in the PMR spectrum are likely due to mechanical or electronic noise. Complex shear modulus $G\left(\omega \right)$ of (C) untreated and (D) ATP-depleted cells. Red circles and blue triangles indicate the real and imaginary parts, respectively. Broken and solid lines indicate the frequency dependency typical of glassy cytoplasms ($\propto {\omega }^{1/2}$) and cytoskeletons ($\propto {\omega }^{3/4}$), respectively. To see this figure in color, go online.

Figure 3

Investigation of the FDT violation. PSD of nonthermal active force $⟨{\left|{\tilde{f}}_{\mathrm{A}}\left(\omega \right)\right|}^2⟩$ measured in (A) untreated and (B) ATP-depleted cells. Circles are the average and bars indicate the log-normal SD. Average values were fitted by $⟨{\left|{\tilde{f}}_{\mathrm{A}}\left(\omega \right)\right|}^2⟩=B{\omega }^{\beta }$ with $\beta =-2$, as shown by the dashed lines. (C) Magnitude of the nonthermal active force $B$ obtained by the fitting. No significant difference was observed, p$=0.41$. (D) $Q\left(t_{\mathrm{e}}\right)$ estimated by the area of green-colored region in Fig. 2A and B. The difference was significant, p$=2.08\times {10}^{-4}$. (C and D) The Mann-Whitney U test was used to calculate the p values. ^∗∗∗p < 0.001. (E) The relative ATP concentration in cells, reproduced with modification from Ref. (13). (F and G) $⟨{\left|\tilde{\upsilon }\left(\omega \right)\right|}^2⟩$ (red circles) and $⟨{\left|{\tilde{\upsilon }}_{\text{th}}\left(\omega \right)\right|}^2⟩=\omega 2k_{\mathrm{B}}T{\alpha }^{″}\left(\omega \right)$ (black circles) of probe particles embedded in (F) untreated and (G) ATP-depleted HeLa cells. In (A), (B), (F), and (G), curves are interpolations and bars indicate the log-normal SD. To see this figure in color, go online.

Figure 4

Microscopic and mesoscopic dynamics of fluctuations. (A) Conventional Langevin model at equilibrium. The thermal stochastic force $f_{\text{th}}\left(t\right)$ drives the movement of the probe particle (${\dot{u}}_{\text{th}}\left(t\right)$) as given in Eq. 2. The colloidal particle accompanies the collective flow field in the medium (broken arrows). The microscopic dynamics of solvent molecules and the motion of the probe particle are mostly “separated,” meaning that they are not directly correlated. (B) Langevin model extended to a nonequilibrium situation. Mechano-enzymes are assumed to act as microscopic objects; i.e., their nonthermal activities are separated from the motion of the probe particle and the collective field in the surrounding medium. The thermal collisions of small solvent molecules and microscopic activities of mechano-enzymes are schematically shown in (C) and (D), respectively. Mesoscopic fluctuations in the medium do not directly correlate with the microscopic dynamics, owing to the nonlinear response of the microscopic processes. To see this figure in color, go online.

Figure 5

In living cells, mechano-enzymes generate mesoscopic fluctuation that directly correlates with their activity. The activity could be, e.g., (A) acto-myosin contraction, (B) transportation of cargo in crowded environment, (C and D) the conformational change of mechano-enzymes. (C) An active mechano-enzyme modeled as force dipole $\kappa \left(t\right)$ and placed at $-\mathit{r}$ from the probe particle induces a force-dipolar collective field ${\mathit{u}}_{\mathbf{A}}\left(t;\mathit{r}\right)$, which the probe particle follows. $\hat{\mathit{n}}$ and $\hat{\mathit{r}}$ are unit vectors orienting the direction of the dipolar force and r, respectively. ${\mathit{u}}_{\mathbf{A}}\left(t;\mathit{r}\right)$ is delayed compared to $\kappa \left(t\right)$ owing to the viscoelasticity of the medium. (D) Response of the collective field ${\mathit{u}}_{\mathbf{A}}\left(t;\mathit{r}\right)$ to $\Delta \left(t\right)$ is instant over cellular length scales (∼μm) and at the timescale where FDT violation is observed (∼Hz). ${\mathit{u}}_{\mathbf{A}}\left(t\right)$ directly correlates with $\Delta \left(t\right)$ over mesoscopic length scales smaller than $\sqrt{\left|G\right|/\rho {\omega }^2}$. (E) Fluctuation of the probe particle in a living cell is driven by a population of mechano-enzymes. Randomly distributed independent mechano-enzymes produce active fluctuations given by Eq. A1. To see this figure in color, go online.

Figure 6

Frequency spectra of the FDT violation expected by the mesoscopic continuum model. (A) Schematic of length $\Delta \left(t\right)$ representing action of a mechano-enzyme, e.g., the conformation of a mechano-enzyme with a typical resting size d. $\Delta \left(t\right)$ typically cycles in ${\tau }_{\mathrm{A}}={\tau }_{\mathrm{b}}+{\tau }_{\mathrm{c}}$ during each enzymatic reaction, which takes place with average frequency $⟨1/\tau ⟩$. Note that the time interval $\tau$ between the successive enzymatic reactions is a stochastic variable, and $⟨1/\tau ⟩$ represents enzymatic activity. The reaction events occur randomly, and the orientation $\hat{\mathit{n}}$ and the position $-\mathit{r}$ of the enzyme from the probe particle is altered stochastically at every catalytic reaction. (B and C) The schematic of the PSD for (B) $⟨{\left|\tilde{\Delta }\left(\omega \right)\right|}^2⟩$ and (C) $⟨{\left|\tilde{\dot{\Delta }}\left(\omega \right)\right|}^2⟩\propto ⟨{\left|{\tilde{\upsilon }}_{\mathrm{A}}\left(\omega \right)\right|}^2⟩$, which were estimated from $\Delta \left(t\right)$ given in (A), by following the discussion in Ref. (66). The green solid curve is the case when there is no yielding. We will discuss later the case when mechano-enzymes drive yielding over a timescale of ${\tau }_{\mathrm{s}}$ (see Figs. 7A and 8D). The spectrum will then be altered for $\omega <1/{\tau }_{\mathrm{s}}$ as shown by the blue and red broken curves, depending on the corresponding ${\tau }_{\mathrm{s}}$. (D) $⟨{\left|{\tilde{\upsilon }}_{\mathrm{A}}\left(\omega \right)\right|}^2⟩$ of 2a = 5 μm colloidal particles embedded in a tightly crosslinked active cytoskeletons (actin/myosin gel), calculated from the data given in Fig. 6 of Ref. (29). $⟨{\left|{\tilde{\upsilon }}_{\mathrm{A}}\left(\omega \right)\right|}^2⟩$ shows a plateau around 1–10 Hz but decreases at both higher and lower frequencies. The frequency dependency was similar to the green solid curve in (C), supporting the model that leads to Eq. A3. In contrast to the living cytoplasm, active diffusion was not observed because the tightly crosslinked actin gel hardly experiences structural relaxations. To see this figure in color, go online.

Figure 7

Schematics describing microscopic and mesoscopic yielding. (A) Microscopic yields (black dipolar arrows on left) do not directly generate mesoscopic flows, whereas they govern mesoscopic viscoelasticity of medium. Correlation between activity of mechano-enzymes $\Delta \left(t\right)$ and mesoscopic flow ${\mathit{u}}_{\mathbf{A}}\left(t\right)$ is maintained in this case; i.e., active diffusion should not occur. (B) Activity of crowded mechano-enzymes $\Delta \left(t\right)$ induces a mesoscopic yield represented by $\Omega \left(t\right)$ that generates a mesoscopic flow in the surrounding medium. The mesoscopic flows generated by $\Delta \left(t\right)$ and $\Omega \left(t\right)$ lose their direct correlation because a plastic yielding is highly nonlinear process, leading to active diffusion. (C) Summary of models. To see this figure in color, go online.

Figure 8

Mesoscopic yielding in glassy medium induces non-thermal fluctuations consistent to experimental obsertvation. (A) Displacement field observed in a thermal glassy system. Displacements of particles during $\sim 0.3{\tau }_{\alpha }$ are shown. The data are taken under the same conditions given in Ref. (87). (B) A close-up image of the subsystem from (A) marked by the dashed square. Only the radial component of displacements is shown. The center of the radial coordinate is chosen to be the blue point in (A). (C) Displacements during a single yield in a zero-temperature system that was subjected to quasi-static shear. The data are from Ref. (86). Structural relaxation in a glassy system leaves permanent displacements similar to the force-dipolar field given in Eq. 16. See supporting material for a detailed description of the numerical setups for (A)–(C). (D) Schematic for typical time evolution of $\Omega \left(t\right)$ representing the mesoscopic yields. We consider here the history of yields that occur at a certain yield location encircled in Fig. 7A and B. Although the orientation of the force dipole representing each yield is randomly distributed in 3D, we describe it in one-dimensional form for brevity. (E) Schematic representation of the typical velocity power spectrum of living cytoplasm, given in Fig. 3E and F. Red and black curves indicate the PSD of the total and thermal velocity fluctuations, respectively. The green curve indicates the nonthermal fluctuations, obtained as the difference between the total and thermal fluctuations. Active diffusion is observed for $\omega <1/{\tau }_{\mathrm{s}}$. On the other hand, we expect that the living cytoplasm is fluid-like for $\omega <1/{\tau }_{\alpha }$, although the frequencies are out of the range measurable with our MR technique. To see this figure in color, go online.