Topological Darkness in Optical Heterostructures: Prediction and Confirmation
- PMID: 37869553
- PMCID: PMC10588908
- DOI: 10.1021/acsphotonics.3c00879
Topological Darkness in Optical Heterostructures: Prediction and Confirmation
Abstract
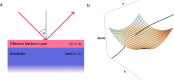
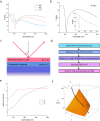
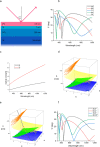
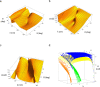
Topological darkness is a new phenomenon that guarantees zero reflection/transmission of light from an optical sample and hence provides topologically nontrivial phase singularities. Here we consider topological darkness in an optical heterostructure that consists of an (unknown) layer placed on a composite substrate and suggest an algorithm that can be used to predict and confirm the presence of topological darkness. The algorithm is based on a combination of optical measurements and the Fresnel equations. We apply this algorithm to ultrathin Pd films fabricated on a Si/SiO2/Cr substrate and extract four different points of topological darkness. Our results will be useful for topological photonics and label-free optical biosensing based on phase interrogation.
© 2023 The Authors. Published by American Chemical Society.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
References
-
- Kravets V. G.; Schedin F.; Jalil R.; Britnell L.; Gorbachev R. V.; Ansell D.; Thackray B.; Novoselov K. S.; Geim A. K.; Kabashin A. V.; Grigorenko A. N. Singular phase nano-optics in plasmonic metamaterials for label-free single-molecule detection. Nat. Mater. 2013, 12, 304–309. 10.1038/nmat3537. - DOI - PubMed
-
- Song H.; Zhang N.; Duan J.; Liu Z.; Gao J.; Singer M. H.; Ji D.; Cheney A. R.; Zeng X.; Chen B.; Jiang S.; Gan Q. Dispersion Topological Darkness at Multiple Wavelengths and Polarization States. Advanced Optical Materials 2017, 5 (12), 170016610.1002/adom.201700166. - DOI
-
- Grigorenko A. N.; Nikitin P. I.; Kabashin A. V. Phase jumps and interferometric surface plasmon resonance imaging. Appl. Phys. Lett. 1999, 75, 3917–3919. 10.1063/1.125493. - DOI
-
- Ermolaev G.; Voronin K.; Baranov D. G.; Kravets V.; Tselikov G.; Stebunov Y.; Yakubovsky D.; Novikov S.; Vyshnevyy A.; Mazitov A.; Kruglov I.; Zhukov S.; Romanov R.; Markeev A. M.; Arsenin A.; Novoselov K. S.; Grigorenko A. N.; Volkov V. Topological phase singularities in atomically thin high-refractive-index materials. Nat. Commun. 2022, 13 (1), 2049.10.1038/s41467-022-29716-4. - DOI - PMC - PubMed
LinkOut - more resources
Full Text Sources
