Universal Pairwise Interatomic van der Waals Potentials Based on Quantum Drude Oscillators

Abstract

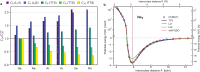
Repulsive short-range and attractive long-range van der Waals (vdW) forces play an appreciable role in the behavior of extended molecular systems. When using empirical force fields, the most popular computational methods applied to such systems, vdW forces are typically described by Lennard-Jones-like potentials, which unfortunately have a limited predictive power. Here, we present a universal parameterization of a quantum-mechanical vdW potential, which requires only two free-atom properties─the static dipole polarizability α₁ and the dipole-dipole C₆ dispersion coefficient. This is achieved by deriving the functional form of the potential from the quantum Drude oscillator (QDO) model, employing scaling laws for the equilibrium distance and the binding energy, and applying the microscopic law of corresponding states. The vdW-QDO potential is shown to be accurate for vdW binding energy curves, as demonstrated by comparing to the ab initio binding curves of 21 noble-gas dimers. The functional form of the vdW-QDO potential has the correct asymptotic behavior at both zero and infinite distances. In addition, it is shown that the damped vdW-QDO potential can accurately describe vdW interactions in dimers consisting of group II elements. Finally, we demonstrate the applicability of the atom-in-molecule vdW-QDO model for predicting accurate dispersion energies for molecular systems. The present work makes an important step toward constructing universal vdW potentials, which could benefit (bio)molecular computational studies.

Figure 1

(a) Errors in the dispersion coefficients arising from the LJ and TTS potentials. The TTS dispersion coefficients are obtained as C_2n = C_2n* × D_eR_e²ⁿ, and the reference dispersion coefficients C_2n^ref are given in Table 1. (b) vdW–QDO potential for neon dimer benchmarked to the TTS potential and the reference CCSD(T) potential. Vertical dotted lines indicate the equilibrium distance as predicted by the CCSD(T) (black) and vdW–QDO potential (red). For comparison, the LJ potentials in two different parameterizations (see our discussion in the text) are also displayed in blue and green.

Figure 2

Potential well depth D_e by eq 17 compared to the reference CCSD(T) values for 21 noble-gas dimers. Mean error (ME) and mean absolute error (MAE) are displayed.

Figure 3

vdW–QDO potentials (solid lines) for (a) homonuclear and (b–d) heteronuclear noble-gas dimers benchmarked to the TTS potential (dashed lines) and the reference CCSD(T) calculations (circles).^,−

Figure 4

(a) Errors in dispersion coefficients predicted by vdW–QDO (dark colors) and TTS (light colors) potentials. (b) Schematic illustration of the Δ_S metric calculation. (c) Heatmaps showing Δ_S (in %) for LJ1 (left) and vdW–QDO (right) potentials with respect to the reference TTS potential. The left and right colorbars have the same scale.

Figure 5

Interatomic potentials of (a) Mg₂, Ca₂, Sr₂, and Ba₂ and of (b) Zn₂, Cd₂, and Hg₂ dimers. The vdW–QDO potentials are shown by solid lines, circles mark coupled-cluster calculations,^,, and crosses display experimental potential curves.⁻

Figure 6

Dimensionless shapes of the vdW–QDO potential curves for Ne₂ (red) and Sr₂ (green) compared with the shapes of the LJ (dashed blue) and TTS (dashed black) potentials.

Figure 7

(a) Dispersion (blue) and exchange (red) contributions to the interaction energy of neopentane dimer (shown as inset) calculated by SAPT–DFT (solid lines) and the damped vdW–QDO potential of eq 27 (dotted lines). In addition, the electrostatic term from SAPT–DFT is displayed in black. (b) Binding energy curves of neopentane dimer as calculated by different methods: CCSD(T) (black); PBE0 + TS (blue) and PBE0 + MBD (green); DFTB3 + MBD (magenta); damped vdW–QDO potential (cyan); SAPT-corrected vdW–QDO potential (eq 30) (red). (c) Errors in the interaction energy of eight dispersion-dominated dimers for the five methods considered. Yellow filling depicts the “chemical accuracy” region of ±1 kcal/mol error.