Ionic Mechanisms of Propagated Repolarization in a One-Dimensional Strand of Human Ventricular Myocyte Model

Abstract

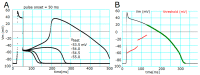
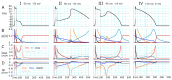
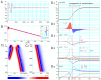
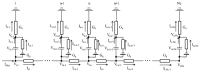
Although repolarization has been suggested to propagate in cardiac tissue both theoretically and experimentally, it has been challenging to estimate how and to what extent the propagation of repolarization contributes to relaxation because repolarization only occurs in the course of membrane excitation in normal hearts. We established a mathematical model of a 1D strand of 600 myocytes stabilized at an equilibrium potential near the plateau potential level by introducing a sustained component of the late sodium current (I_NaL). By applying a hyperpolarizing stimulus to a small part of the strand, we succeeded in inducing repolarization which propagated along the strand at a velocity of 1~2 cm/s. The ionic mechanisms responsible for repolarization at the myocyte level, i.e., the deactivation of both the I_NaL and the L-type calcium current (I_CaL), and the activation of the rapid component of delayed rectifier potassium current (I_Kr) and the inward rectifier potassium channel (I_K1), were found to be important for the propagation of repolarization in the myocyte strand. Using an analogy with progressive activation of the sodium current (I_Na) in the propagation of excitation, regenerative activation of the predominant magnitude of I_K1 makes the myocytes at the wave front start repolarization in succession through the electrical coupling via gap junction channels.

Keywords: early afterdepolarization; human ventricular myocyte; late sodium current; mathematical 1D strand model; repolarization propagation.

Figure 1

Threshold potentials detected by applying V_t of 5 ms in duration to different levels in the hVC model. (A) The application of V_t to −53.5, −54, −54.5, and −55 mV induced dynamic changes in the time course of plateau potential as displayed from top to bottom (four traces), respectively. The black vertical line in panel A indicates the off time (t = 55 ms) of the 5 ms clamp pulse. (B) The threshold potentials at which the given clamp pulse induced abolition of the plateau potential (red) were plotted against the off time of various test pulses. Green dots indicated there were no threshold potential. In this range colored in green, V_t did not induce all-or-none repolarization but led to monotonic repolarization.

Figure 2

Ionic mechanisms underlying changes in V_m induced by applying 5 ms hyperpolarizing clamp pulses. Each time and voltage of the brief hyperpolarizing voltage clamp pulse applied were indicated at the top of each column. (A) indicates V_m, (B) indicates the open probabilities p(O) of currents, I_K1 (red), I_Kr (steel blue), I_Kto (black), I_CaL multiplied by 2 (chocolate), and I_NaL multiplied by 100 (blue), (C,D) indicate amplitudes of outward (I_out) and inward (I_in) currents, respectively. The same colors were used as in (B). The sum of major outward and inward currents was calculated and illustrated in gray. The amplitude of I_NaK (pink) and I_bNSC (black) are also shown in (C) and (D), respectively. The vertical lines indicate the end of the clamp pulse.

Figure 3

The N-shaped I-V curve with two stable equilibrium potentials and one unstable equilibrium potential of the hVC model. The I-V curves in (A,C1,C2) were measured by applying the voltage clamp test pulses of 4.9 s in duration given every 2 mV step from the holding potential of −80 mV. Current magnitudes saturated within the duration of test pulses at the end of individual test pulses, and were plotted in these figures. Additionally, (A) shows total whole cell current (black) and current components I_K1, I_Kr, I_NaL, and I_CaL depicted in different colors as indicated. The steady-state p(O)s of major ion channels were plotted in (B). Note that p(O)_INaL and p(O)_ICaL were plotted after multiplication by 100 and 10, respectively. (C1,C2) shows the influence of increasing the amplitude of I_NaL on the appearance of equilibrium points in the presence and the absence of I_CaL, respectively. Increasing the amplitude of I_NaL shifted the N-shaped I-V curve negatively. All I-V and p(O)-V relationships share the same abscissa of V_m. In (D), the state of slow inactivation, I_s and the transitional inactivated state, I₂ of I_NaL, were shaded by gray color to indicate that these states were frozen, namely, the state transition from other states was totally prevented as indicated by cross marks. Thereby, repetitive state transitions between I₁ and O produce continuous bursts of brief openings of the channel, and ‘late scattered mode’ of Na channel [16] (k_I1O is close to k_OI1) during a clamp pulse to depolarized potentials. If integrated over bursts with numerous numbers of brief openings, the whole-cell I_NaL maintains a significant amplitude during depolarization. With an intact transition scheme, I_NaL gradually decreases in amplitude through the state transition from O to (I_s + I₂) when the membrane is depolarized. The state transition between the two closed states (C1,C2) was assumed to be instantaneous on the V_m jump; the probability of (C2) increases with membrane depolarization. In the state transition of transient sodium current (I_NaT) (see Supplementary Materials) the I₁ state is absent, and the inactivation occurs through a state transition from O to I₂ at transition rate k_OI2, which has the same magnitude as k_OI1.

Figure 4

Propagated repolarization in a linear strand of the EAD-prone myocytes in comparison to that of excitation. Panel A shows the time course of V_m, moving from the resting membrane potential (−91 mV) to the second stable equilibrium potential (−2 mV) in the myocyte strand, in which the deeply inactivated states (I_s + I₂) of I_NaL were removed. Panel (A) indicates V_m recordings in cell No. 1 (blue) and 17 (red). The AP was evoked by applying a depolarizing pulse to cell No. 1 in the 1D strand of the hVC model. The V_m stabilized at about −3 mV at the end of the record in all myocytes within the strand. Panel (B) indicates the propagation of the O/I pattern (propagation of excitation) along the myocyte strand. The inset shows the stable O/I pattern of V_o; positive V_o evoked by outward whole-cell current, I_o (red), or negative V_o due to inward I_o (blue). Note, that the cell number on the abscissa of the inset is the same as in panel B, but the scale of the V_o is reduced by 100 times. Panels (B,C) indicate the movement of O/I patterns (propagation of repolarization) along the myocyte strand by using the color code of V_o shown at the bottom of panel (C). The O/I patterns illustrated in (C1,C2) were obtained at different recording times. See text for the explanation of panels (D1–D5). Note that p(O)_INaL and p(O)_ICaL were plotted after multiplication by 100 and 10, respectively, in panel (D5). The time scale shown in (D5) is common for all (D1–D5). The arrow head in (D1) indicates the direction of the propagation of repolarization. The scaling factor of I_K1 = 1.2 was used in this simulation. Note that the scale of the V_o is reduced by 100 times in panel (C) if compared to that in panel (B).

Figure 5

The electrically equivalent circuit of the myocyte strand. G_o; the extracellular conductance of 10 µS, V_o; extracellular potential near the cell surface, C_m; membrane capacitance of 192.5 pF, V_m; membrane potential, V_i; intracellular potential, I_o; extracellular current, I_c; capacitor current, I_m; membrane current, I_i; gap junction current, G_g; the gap junction conductance of 1.5 µS assumed for the end-to-end junction along the longitudinal axis of the cuboid shape myocyte.