Quantum Honeypots

Abstract

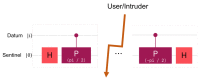
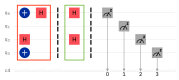
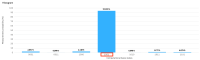
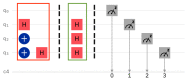
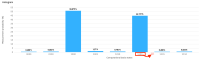
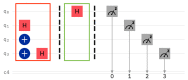
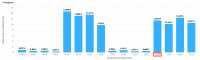
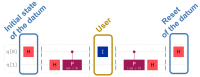
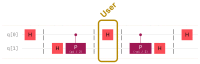
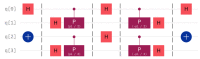
Quantum computation offers unique properties that cannot be paralleled by conventional computers. In particular, reading qubits may change their state and thus signal the presence of an intruder. This paper develops a proof-of-concept for a quantum honeypot that allows the detection of intruders on reading. The idea is to place quantum sentinels within all resources offered within the honeypot. Additional to classical honeypots, honeypots with quantum sentinels can trace the reading activity of the intruder within any resource. Sentinels can be set to be either visible and accessible to the intruder or hidden and unknown to intruders. Catching the intruder using quantum sentinels has a low theoretical probability per sentinel, but the probability can be increased arbitrarily higher by adding more sentinels. The main contributions of this paper are that the monitoring of the intruder can be carried out at the level of the information unit, such as the bit, and quantum monitoring activity is fully hidden from the intruder. Practical experiments, as performed in this research, show that the error rate of quantum computers has to be considerably reduced before implementations of this concept are feasible.

Keywords: honeypot; post-quantum security; quantum networks; quantum security.

Figure 1

The hidden sentinel is the second qubit in the figure. It is acted on by the datum sentinel via the control of phase shift gates. The middle of the figure shows the area and time when the datum-qubit is exposed to the user.

Figure 2

The legal user measures the sentinels in the correct bases.

Figure 3

The measurement probability of Figure 2, which has four sentinels, and the user is legal.

Figure 4

Experiment with four positional sentinels. The intruder’s behavior is random, as the state of the sentinels is not known to the user. In this particular case, the intruder makes a mistake on $q_2$ and, therefore, the detection probability is theoretically $\frac{1}{2}$.

Figure 5

The measurement probability of Figure 4, which contains four positional sentinels, and the intruder misses one.

Figure 6

Four positional sentinels are set to all possible values. The experiment shows the option where the intruder is lucky on only one qubit, namely $q_2$.

Figure 7

The measurement probability of Figure 6 with four positional sentinels and the intruder missing three of the sentinels. The result in red refers to the probability of the intruder to escape detection.

Figure 8

Legal user reading a datum qubit with a hidden sentinel. The same circuit applies to a lucky intruder. The user does not disturb the state of the datum qubit.

Figure 9

Unlucky intruder reading a quantum qubit with a hidden sentinel. In the case of an unlucky intruder, an extra Hadamard gate on the datum qubit disturbs the hidden sentinel.

Figure 10

The circuit with two active hidden sentinels shows an intruder that has wrongly measured two datum qubits, $q_0$ and $q_2$, that act on two hidden sentinels, $q_1$ and $q_3$.

Figure 11

The left panel shows the practical results obtained on running a circuit with two hidden sentinels. The panel on the right shows the theoretical expectation.