Mixing Linear Polymers with Rings and Catenanes: Bulk and Interfacial Behavior
- PMID: 37900098
- PMCID: PMC10601540
- DOI: 10.1021/acs.macromol.3c01267
Mixing Linear Polymers with Rings and Catenanes: Bulk and Interfacial Behavior
Abstract
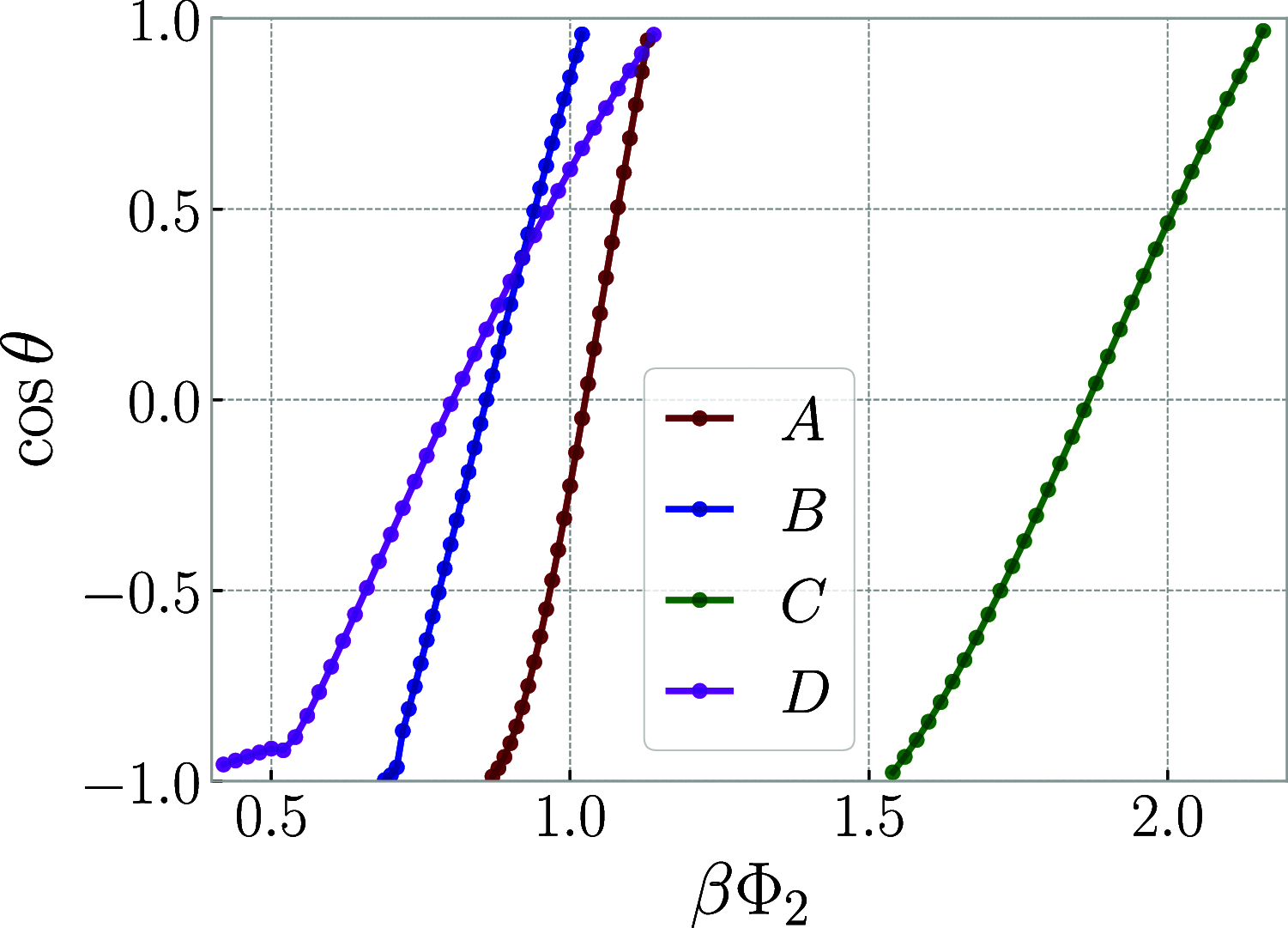
We derive and parameterize effective interaction potentials between a multitude of different types of ring polymers and linear chains, varying the bending rigidity and solvent quality for the former species. We further develop and apply a density functional treatment for mixtures of both disconnected (chain-ring) and connected (chain-polycatenane) mixtures of the same, drawing coexistence binodals and exploring the ensuing response functions as well as the interface and wetting behavior of the mixtures. We show that worsening of the solvent quality for the rings brings about a stronger propensity for macroscopic phase separation in the linear-polycatenane mixtures, which is predominantly of the demixing type between phases of similar overall particle density. We formulate a simple criterion based on the effective interactions, allowing us to determine whether any specific linear-ring mixture will undergo a demixing phase separation.
© 2023 The Authors. Published by American Chemical Society.
Conflict of interest statement
The authors declare no competing financial interest.
Figures

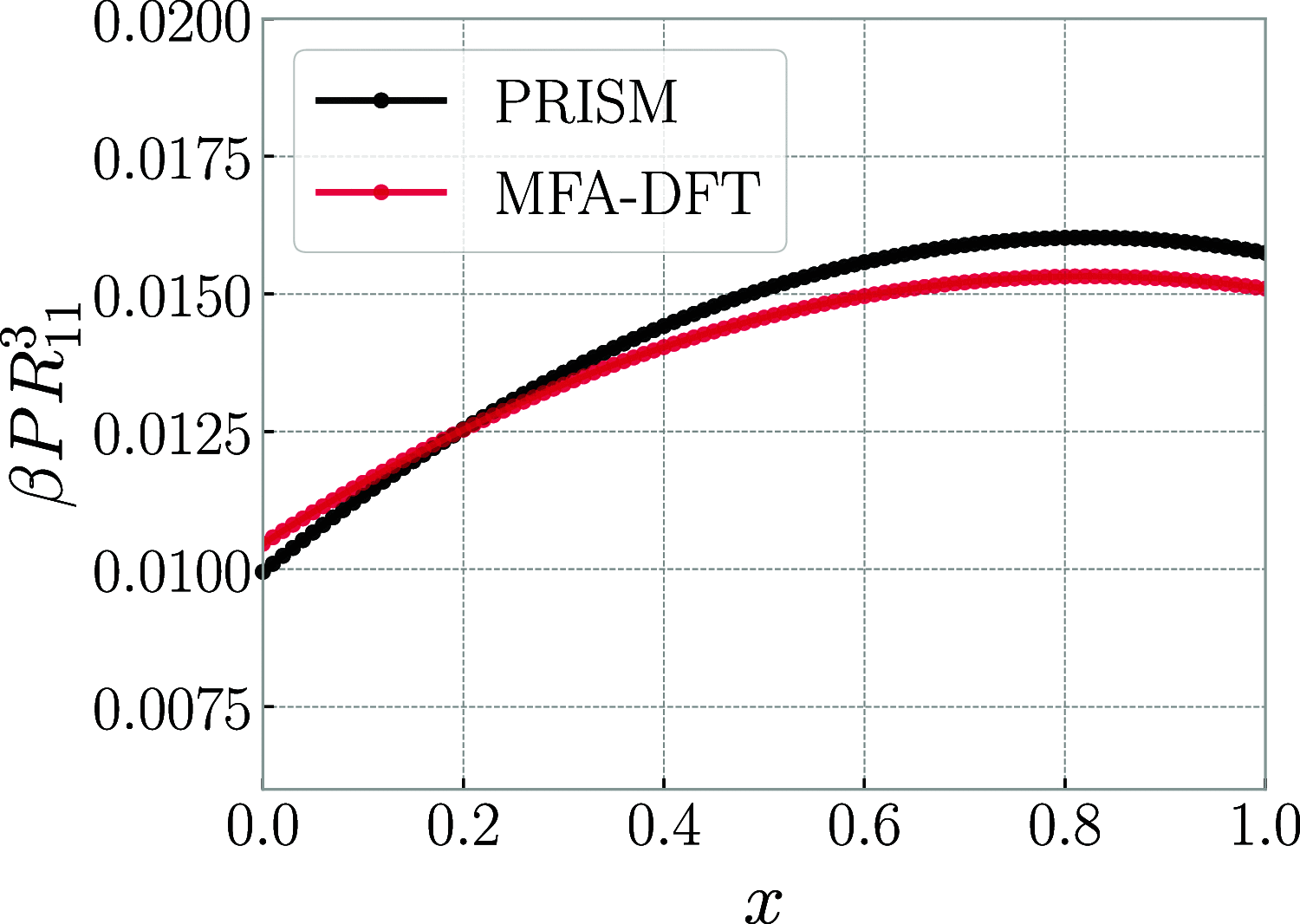


References
-
- Polymeropoulos G.; Zapsas G.; Ntetsikas K.; Bilalis P.; Gnanou Y.; Hadjichristidis N. 50th Anniversary Perspective: Polymers with Complex Architectures. Macromolecules 2017, 50, 1253–1290. 10.1021/acs.macromol.6b02569. - DOI
-
- Micheletti C.; Marenduzzo D.; Orlandini E. Polymers with spatial or topological constraints: Theoretical and computational results. Phys. Rep. 2011, 504, 1–73. 10.1016/j.physrep.2011.03.003. - DOI
-
- Rubinstein M.; Colby R. H.. Polymer Physics; Oxford University Press, 2003.
LinkOut - more resources
Full Text Sources
