This is a preprint.
Mechanical coupling coordinates microtubule growth
- PMID: 37905093
- PMCID: PMC10614740
- DOI: 10.1101/2023.06.29.547092
Mechanical coupling coordinates microtubule growth
Update in
-
Mechanical coupling coordinates microtubule growth.Elife. 2023 Dec 27;12:RP89467. doi: 10.7554/eLife.89467. Elife. 2023. PMID: 38150374 Free PMC article.
Abstract
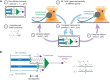
During mitosis, kinetochore-attached microtubules form bundles (k-fibers) in which many filaments grow and shorten in near-perfect unison to align and segregate each chromosome. However, individual microtubules grow at intrinsically variable rates, which must be tightly regulated for a k-fiber to behave as a single unit. This exquisite coordination might be achieved biochemically, via selective binding of polymerases and depolymerases, or mechanically, because k-fiber microtubules are coupled through a shared load that influences their growth. Here, we use a novel dual laser trap assay to show that microtubule pairs growing in vitro are coordinated by mechanical coupling. Kinetic analyses show that microtubule growth is interrupted by stochastic, force-dependent pauses and indicate persistent heterogeneity in growth speed during non-pauses. A simple model incorporating both force-dependent pausing and persistent growth speed heterogeneity explains the measured coordination of microtubule pairs without any free fit parameters. Our findings illustrate how microtubule growth may be synchronized during mitosis and provide a basis for modeling k-fiber bundles with three or more microtubules, as found in many eukaryotes.
Figures
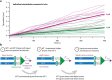
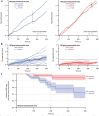
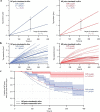
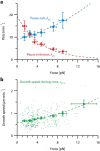
 ) and exit (
) and exit ( ) rates (kEN and kEX) were estimated as described in Figure S5–1 and are plotted as functions of force. Error bars show counting uncertainties from N = 25 to 85 individual microtubule recordings and dashed curves show least squares exponential fits. (b) As tension on a microtubule tip increases, the growth during runs (i.e., in-between pauses) is accelerated. Points show run speeds measured from recordings of individual microtubules subject to constant tensile forces (from (Akiyoshi et al., 2010)). Symbols (
) rates (kEN and kEX) were estimated as described in Figure S5–1 and are plotted as functions of force. Error bars show counting uncertainties from N = 25 to 85 individual microtubule recordings and dashed curves show least squares exponential fits. (b) As tension on a microtubule tip increases, the growth during runs (i.e., in-between pauses) is accelerated. Points show run speeds measured from recordings of individual microtubules subject to constant tensile forces (from (Akiyoshi et al., 2010)). Symbols ( ) represent mean run speeds (vRUN) grouped according to the applied tensile force. Error bars show SEMs from N = 9 to 85 individual microtubule recordings and dashed curve shows the least squares exponential fit. See Figure S5–1 and Materials and Methods for details and Table 1 for fit parameters.
) represent mean run speeds (vRUN) grouped according to the applied tensile force. Error bars show SEMs from N = 9 to 85 individual microtubule recordings and dashed curve shows the least squares exponential fit. See Figure S5–1 and Materials and Methods for details and Table 1 for fit parameters.
Similar articles
-
Mechanical coupling coordinates microtubule growth.Elife. 2023 Dec 27;12:RP89467. doi: 10.7554/eLife.89467. Elife. 2023. PMID: 38150374 Free PMC article.
-
The microtubule-associated protein HURP recruits the centrosomal protein TACC3 to regulate K-fiber formation and support chromosome congression.J Biol Chem. 2018 Oct 5;293(40):15733-15747. doi: 10.1074/jbc.RA118.003676. Epub 2018 Jul 27. J Biol Chem. 2018. PMID: 30054275 Free PMC article.
-
PRC1-labeled microtubule bundles and kinetochore pairs show one-to-one association in metaphase.EMBO Rep. 2017 Feb;18(2):217-230. doi: 10.15252/embr.201642650. Epub 2016 Dec 27. EMBO Rep. 2017. PMID: 28028032 Free PMC article.
-
The dynamic kinetochore-microtubule interface.J Cell Sci. 2004 Nov 1;117(Pt 23):5461-77. doi: 10.1242/jcs.01536. J Cell Sci. 2004. PMID: 15509863 Review.
-
Mechanisms of Chromosome Congression during Mitosis.Biology (Basel). 2017 Feb 17;6(1):13. doi: 10.3390/biology6010013. Biology (Basel). 2017. PMID: 28218637 Free PMC article. Review.
References
-
- Akiyoshi B., Sarangapani K. K., Powers A. F., Nelson C. R., Reichow S. L., Arellano-Santoyo H., Gonen T., Ranish J. A., Asbury C. L., & Biggins S. (2010). Tension directly stabilizes reconstituted kinetochore-microtubule attachments. Nature, 468(7323), 576–579. 10.1038/nature09594 - DOI - PMC - PubMed
-
- Amin M. A., Agarwal S., & Varma D. (2019). Mapping the kinetochore MAP functions required for stabilizing microtubule attachments to chromosomes during metaphase. Cytoskeleton, 76(6), 398–412. https://doi.org/10.1002%2Fcm.21559 - PMC - PubMed
Publication types
Associated data
Grants and funding
LinkOut - more resources
Full Text Sources
