Evidence for ground state coherence in a two-dimensional Kondo lattice

Abstract

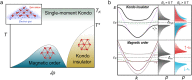
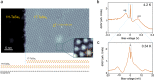
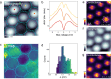
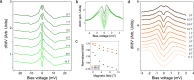
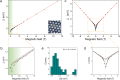
Kondo lattices are ideal testbeds for the exploration of heavy-fermion quantum phases of matter. While our understanding of Kondo lattices has traditionally relied on complex bulk f-electron systems, transition metal dichalcogenide heterobilayers have recently emerged as simple, accessible and tunable 2D Kondo lattice platforms where, however, their ground state remains to be established. Here we present evidence of a coherent ground state in the 1T/1H-TaSe₂ heterobilayer by means of scanning tunneling microscopy/spectroscopy at 340 mK. Our measurements reveal the existence of two symmetric electronic resonances around the Fermi energy, a hallmark of coherence in the spin lattice. Spectroscopic imaging locates both resonances at the central Ta atom of the charge density wave of the 1T phase, where the localized magnetic moment is held. Furthermore, the evolution of the electronic structure with the magnetic field reveals a non-linear increase of the energy separation between the electronic resonances. Aided by ab initio and auxiliary-fermion mean-field calculations, we demonstrate that this behavior is inconsistent with a fully screened Kondo lattice, and suggests a ground state with magnetic order mediated by conduction electrons. The manifestation of magnetic coherence in TMD-based 2D Kondo lattices enables the exploration of magnetic quantum criticality, Kondo breakdown transitions and unconventional superconductivity in the strict two-dimensional limit.

Fig. 1. Ground state of a Kondo lattice.

a Doniach phase diagram of a Kondo lattice showing its two possible electronic ground states at low temperatures, the magnetic order and Kondo insulator. The inset shows a representation of the spin lattice (red) and the itinerant electron gas from the metal (blue). J is the local exchange coupling between the localized magnetic moment and the conduction electrons. b Schematic band structures and spin-resolved (z component) density of states (ρ) of the two ground states. In a Kondo insulator (upper panel), the conduction band (purple curve) and the localized states (green curve) hybridize to form two spin-degenerate electronic bands (black curves) separated by a gap (Δ_hyb). If the Kondo lattice develops magnetic order (lower panel), spin-polarized electronic bands emerge around E_F, which leads to two peaks in ρ separated by Δ_m. In the presence of an external magnetic field in the out-of-plane direction, however, ρ develops differently and both ground states can be distinguished.

Fig. 2. Atomic and electronic structure of the 1T-TaSe₂/1H-TaSe₂ heterobilayer.

a Large-scale STM image of a monolayer of 1T-TaSe₂ on monolayer 1H-TaSe₂ grown on BLG/SiC(0001) (V_s = −2 V, I = 0.08 nA, T = 4.2 K). Below a sketch of the vertical arrangement of the atomic layer is shown. Se, Ta, and C atoms are displayed in orange, yellow, and black, respectively. The inset shows a high-resolution STM image of the CDW supercell, where a sketch of the SoD is overlaid (V_s = −2.5 mV, I = 2 nA, T = 0.34 K). b Typical dI/dV spectrum taken on the 1T/1H heterostructure at 4.2 K (V_a.c. = 1 mV). The position of the lower (upper) Hubbard bands are indicated. c Low-bias dI/dV spectrum acquired on the 1T/1H heterostructure at our base temperature of 0.34 K showing the emergence of two peaks (V_a.c. = 50 µV, B = 0 T). The energy separation (Δ) between the peaks maxima is indicated.

Fig. 3. Spatial mapping of the low-energy electronic structure.

a STM topography of the 1T/1H heterostructure (V_s = 4 mV, I = 1.5 nA, T = 0.34 K, 3.3 × 3.3 nm²). The blue circles represent the boundaries of the Star-of-David clusters. b dI/dV spectra taken at the center of the three neighboring clusters indicated dots in (a) (V_a.c. = 40 µV, B = 0 T). c Spatially resolved map (32 × 32 pixel, raw data) of Δ (separation of peaks) taken in the region shown in (a). The map is extracted from a 40 × 40 dI/dV grid acquired at 0.34 K (V_a.c. = 40 µV, B = 0 T). The color scale of the Δ map is shown in the histogram in (d). e Conductance map (constant height) acquired at V_s = +1 mV and I = 0.16 nA. The atomic position of the SoD cluster is indicated. f Topograph of the region where the conductance maps were taken (V_s = −5 mV, I = 0.18 nA). g Conductance map at the opposite polarity (V_s = −1 mV, I = 0.2 nA) in the same region (for both conductance maps: V_a.c. = 20 µV, B = 0 T, T = 0.34 K).

Fig. 4. Magnetic-field dependence of the low-energy electronic structure.

a Set of dI/dV spectra taken consecutively at T = 0.34 K as the perpendicular magnetic field is varied in the 0–11 T range (V_a.c = 50 µV). b Zoom-in of the set shown in (a). The curves are normalized to the set-point voltage (V_b = + 25 mV). c Differential conductance values measured at the peaks maxima (E⁺(orange circles) and E⁻ (brown circles)) and E_F (blue triangles) in the dI/dV spectra shown in (a). d High-resolution series of dI/dV spectra taken consecutively at T = 0.34 K in the vicinity of E_F (V_a.c. = 30 µV).

Fig. 5. Non-linear behavior of Δ with the magnetic field.

a Plot of Δ as a function of B_z for a series of dI/dV spectra taken consecutively in the SoD cluster shown in the inset. The red dashed line is the linear fit realized in the 1 T < B_z < 11 T. The green shadow indicates the range of B_Z where Δ deviates from a linear relation. The insert shows the SoD (encircled) where the data were taken. b Zoom-in of the boxed region in (a). The gray region indicates the uncertainty band of Δ in the linear region (see SI). c Plot of Δ as a function of B_z for a series of dI/dV spectra taken consecutively in the range ±11 T. The red dashed lines are the linear fits. d Zoom-in of the boxed region in (c). e Histogram showing the occurrence of $∣S∣$ for the different SoD clusters explored within 0 T < B_z < 11 T.

Fig. 6. Splitting patterns from mean-field f~-fermion description.

a Schematic dependence of the spectral function with out-of-plane ferromagnetic order, for different values of the field in integer multiples of $B_{\max }=J_K{S}_c^{\max }/g{\mu }_B$. At low fields, the peak splitting decreases when the field polarity is opposite to the narrow band magnetization, but it increases when they are aligned. b Spectral function with in-plane order. The peaks split symmetrically with magnetic field polarity. c Non-linear behavior of the gap for the in-plane case due to the reorientation and increased magnitude of the magnetic moment as the field is applied, for $S_c^{\max }$= 0.077, $B_c=0.5\mathrm{T}$ and different values of the initial moment $S_c^0$.