Sedimentation of a Charged Spherical Particle in a Viscoelastic Electrolyte Solution
- PMID: 37930108
- PMCID: PMC10778095
- DOI: 10.1021/acs.langmuir.3c02102
Sedimentation of a Charged Spherical Particle in a Viscoelastic Electrolyte Solution
Abstract
When a charged particle translates through an electrolyte solution, the electric double layer around it deforms in response to the fluid motion and creates an electric force opposite the direction of motion, decreasing the settling velocity. This is a multidisciplinary phenomenon that combines fluid mechanics and electrodynamics, differentiating it from the classical problem of an uncharged sedimenting particle. It has many applications varying from mechanical to biomedical, such as in drug delivery in blood through charged microparticles. Related studies so far have focused on Newtonian fluids, but recent studies have proven that many biofluids, such as human blood plasma, have elastic properties. To this end, we perform a computational study of the steady sedimentation of a spherical, charged particle in human blood plasma due to the centrifugal force. We used the Giesekus model to describe the rheological behavior of human blood plasma. Assuming axial symmetry, the governing equations include the momentum and mass balances, Poisson's equation for the electric field, and the species conservation. The finite size of the ions is considered through the local-density approximation approach of Carnahan-Starling. We perform a detailed parametric analysis, varying parameters such as the ζ potential, the size of the ions, and the centrifugal force exerted upon the particle. We observe that as the ζ potential increases, the settling velocity decreases due to a stronger electric force that slows the particle. We also conduct a parametric analysis of the relaxation time of the material to investigate what happens generally in viscoelastic electrolyte solutions and not only in human blood plasma. We conclude that elasticity plays a crucial role and should not be excluded from the study. Finally, we examine under which conditions the assumption of point-like ions gives different predictions from the Carnahan-Starling approach.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
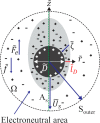
 , which in this study
is a centrifugal force.
Here, Ω represents the area that the viscoelastic material occupies. As and Souter denote
the axis of symmetry and the far-field boundary, respectively.
, which in this study
is a centrifugal force.
Here, Ω represents the area that the viscoelastic material occupies. As and Souter denote
the axis of symmetry and the far-field boundary, respectively.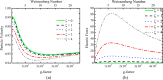
 , on
(a) the particle velocity and (b) the
electric force for different values of ζ and ΦB = 0. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
, on
(a) the particle velocity and (b) the
electric force for different values of ζ and ΦB = 0. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
 , (Wi = 0.58) and (b)
, (Wi = 0.58) and (b)  , (Wi = 23.232), when ζ
= 3 and ΦB = 0. Τhe extent of the EDL is indicated
by the white dashed lines. The particle is sedimenting in blood plasma
which follows the Giesekus model using the parameters of Table 2.
, (Wi = 23.232), when ζ
= 3 and ΦB = 0. Τhe extent of the EDL is indicated
by the white dashed lines. The particle is sedimenting in blood plasma
which follows the Giesekus model using the parameters of Table 2.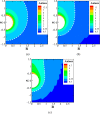
 , (Wi = 2.56), (b)
, (Wi = 2.56), (b)  , (Wi = 9.16), and (c)
, (Wi = 9.16), and (c)  , (Wi = 23.232) when ζ
= 3 and ΦB = 0. The particle is sedimenting in blood
plasma which follows the Giesekus model using the parameters of Table 2.
, (Wi = 23.232) when ζ
= 3 and ΦB = 0. The particle is sedimenting in blood
plasma which follows the Giesekus model using the parameters of Table 2.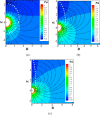
 , (Wi = 2.56), (b)
, (Wi = 2.56), (b)  , (Wi = 9.16), and (c)
, (Wi = 9.16), and (c)  , (Wi = 23.232), when ζ
= 3 and ΦB = 0. The particle is sedimenting in blood
plasma which follows the Giesekus model using the parameters of Table 2.
, (Wi = 23.232), when ζ
= 3 and ΦB = 0. The particle is sedimenting in blood
plasma which follows the Giesekus model using the parameters of Table 2.
 for different values of ζ and ΦB = 0. The particle is sedimenting in a viscoelastic material
that follows the Giesekus model using the parameters of Table 2. Only the relaxation time varies
here.
for different values of ζ and ΦB = 0. The particle is sedimenting in a viscoelastic material
that follows the Giesekus model using the parameters of Table 2. Only the relaxation time varies
here.
 , (Wi = 0.528) and (b)
, (Wi = 0.528) and (b)  , (Wi = 5.28). The particle
is sedimenting in blood plasma which follows the Giesekus model using
the parameters of Table 2.
, (Wi = 5.28). The particle
is sedimenting in blood plasma which follows the Giesekus model using
the parameters of Table 2.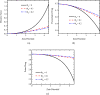
 , (Wi = 5.28). The particle
is sedimenting in blood plasma which follows the Giesekus model using
the parameters of Table 2.
, (Wi = 5.28). The particle
is sedimenting in blood plasma which follows the Giesekus model using
the parameters of Table 2.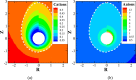
 , (Wi = 5.28) when ζ
= 3, (a) cations and (b) anions. The left-hand side of each panel
corresponds to ΦB = 0.2, and the right-hand side
corresponds to ΦB = 0. The particle is sedimenting
in blood plasma which follows the Giesekus model using the parameters
of Table 2.
, (Wi = 5.28) when ζ
= 3, (a) cations and (b) anions. The left-hand side of each panel
corresponds to ΦB = 0.2, and the right-hand side
corresponds to ΦB = 0. The particle is sedimenting
in blood plasma which follows the Giesekus model using the parameters
of Table 2.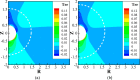
 , (Wi = 0.528) and for
two different values of zeta potentials: (a) ζ = 2 and (b) ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
, (Wi = 0.528) and for
two different values of zeta potentials: (a) ζ = 2 and (b) ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
 , Wi = 0.528 and for two
different values of zeta potential: (a) ζ = 2 and (b) ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
, Wi = 0.528 and for two
different values of zeta potential: (a) ζ = 2 and (b) ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
 , Wi = 0.528 and for two
different values of zeta potential: (a) ζ = 2 and (b) ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
, Wi = 0.528 and for two
different values of zeta potential: (a) ζ = 2 and (b) ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
 , (Wi = 0.528) and (b)
, (Wi = 0.528) and (b)  , (Wi = 5.28). The particle
is sedimenting in blood plasma which follows the Giesekus model using
the parameters of Table 2.
, (Wi = 5.28). The particle
is sedimenting in blood plasma which follows the Giesekus model using
the parameters of Table 2.
 , Wi = 0.528 with ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
, Wi = 0.528 with ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.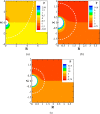
 , (Wi = 0.528) with ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
, (Wi = 0.528) with ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
 (Wi = 0.528) and ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
(Wi = 0.528) and ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
 , (Wi = 0.528) with ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
, (Wi = 0.528) with ζ
= 4. The particle is sedimenting in blood plasma which follows the
Giesekus model using the parameters of Table 2.
 and the other dimensionless numbers is
summarized in Table A1. (b) Mesh convergence for the Newtonian material for ζ = 4
and for three different meshes (Table A2) and (c) mesh convergence validation for
the viscoelastic material for ζ = 3 and for three different
meshes (Table A2).
and the other dimensionless numbers is
summarized in Table A1. (b) Mesh convergence for the Newtonian material for ζ = 4
and for three different meshes (Table A2) and (c) mesh convergence validation for
the viscoelastic material for ζ = 3 and for three different
meshes (Table A2).Similar articles
-
Sedimentation of a charged colloidal sphere in a charged cavity.J Chem Phys. 2011 Dec 7;135(21):214706. doi: 10.1063/1.3663380. J Chem Phys. 2011. PMID: 22149810
-
Settling of a charged hydrophobic rigid colloid in aqueous media under generalized gravitational field.Electrophoresis. 2021 Apr;42(7-8):1010-1020. doi: 10.1002/elps.202000240. Epub 2020 Nov 30. Electrophoresis. 2021. PMID: 33159354
-
Sedimentation of a Charged Soft Sphere within a Charged Spherical Cavity.Molecules. 2024 Jun 28;29(13):3087. doi: 10.3390/molecules29133087. Molecules. 2024. PMID: 38999039 Free PMC article.
-
Sedimentation of a charged porous particle in a charged cavity.J Phys Chem B. 2013 Oct 10;117(40):12319-27. doi: 10.1021/jp407805x. Epub 2013 Sep 27. J Phys Chem B. 2013. PMID: 24041255
-
Numerical analysis of thermophoresis of charged colloidal particles in non-Newtonian concentrated electrolyte solutions.Electrophoresis. 2022 Nov;43(21-22):2267-2275. doi: 10.1002/elps.202200030. Epub 2022 Jun 9. Electrophoresis. 2022. PMID: 35589398
References
-
- Masliyah J. H.; Bhattacharjee S.. Electrokinetic and Colloid Transport Phenomena; John Wiley & Sons, 2006.
-
- Barbero F.; Russo L.; Vitali M.; Piella J.; Salvo I.; Borrajo M. L.; Busquets-Fité M.; Grandori R.; Bastús N. G.; Casals E.; Puntes V. Formation of the Protein Corona: The Interface between Nanoparticles and the Immune System. Semin. Immunol. 2017, 34 (October), 52–60. 10.1016/j.smim.2017.10.001. - DOI - PubMed
-
- Hiemenz P. C.; Rajagopalan R.. Principles of Colloid and Surface Chemistry; CRC Press, 2016.
LinkOut - more resources
Full Text Sources

