Unified topological inference for brain networks in temporal lobe epilepsy using the Wasserstein distance
- PMID: 37931870
- PMCID: PMC11074922
- DOI: 10.1016/j.neuroimage.2023.120436
Unified topological inference for brain networks in temporal lobe epilepsy using the Wasserstein distance
Abstract
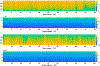
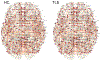
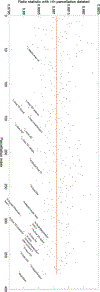
Persistent homology offers a powerful tool for extracting hidden topological signals from brain networks. It captures the evolution of topological structures across multiple scales, known as filtrations, thereby revealing topological features that persist over these scales. These features are summarized in persistence diagrams, and their dissimilarity is quantified using the Wasserstein distance. However, the Wasserstein distance does not follow a known distribution, posing challenges for the application of existing parametric statistical models. To tackle this issue, we introduce a unified topological inference framework centered on the Wasserstein distance. Our approach has no explicit model and distributional assumptions. The inference is performed in a completely data driven fashion. We apply this method to resting-state functional magnetic resonance images (rs-fMRI) of temporal lobe epilepsy patients collected from two different sites: the University of Wisconsin-Madison and the Medical College of Wisconsin. Importantly, our topological method is robust to variations due to sex and image acquisition, obviating the need to account for these variables as nuisance covariates. We successfully localize the brain regions that contribute the most to topological differences. A MATLAB package used for all analyses in this study is available at https://github.com/laplcebeltrami/PH-STAT.
Copyright © 2023. Published by Elsevier Inc.
Conflict of interest statement
Declaration of competing interest The study was approved and follows the University of Wisconsin-Madison and Medical College of Wisconsin IRB protocols. The study was conducted ethically following the IRB protocol. The epilepsy data is not available due to the IRB protocol.
Figures



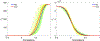





Update of
-
Unified Topological Inference for Brain Networks in Temporal Lobe Epilepsy Using the Wasserstein Distance.ArXiv [Preprint]. 2023 Sep 20:arXiv:2302.06673v3. ArXiv. 2023. Update in: Neuroimage. 2023 Dec 15;284:120436. doi: 10.1016/j.neuroimage.2023.120436. PMID: 36824424 Free PMC article. Updated. Preprint.
References
-
- Abdallah H, Regalski A, Kang MB, Berishaj M, Nnadi N, Chowdury A, Diwadkar VA, Salch A, 2023. Statistical inference for persistent homology applied to simulated fMRI time series data. Found. Data Sci 5, 1–25.
-
- Adams H, Emerson T, Kirby M, Neville R, Peterson C, Shipman P, Chepushtanova S, Hanson E, Motta F, Ziegelmeier L, 2017. Persistence images: A stable vector representation of persistent homology. J. Mach. Learn. Res 18, 218–252.
-
- Adler RJ, Bobrowski O, Borman MS, Subag E, Weinberger S, 2010. Persistent homology for random fields and complexes. In: Borrowing Strength: Theory Powering Applications-a Festschrift for Lawrence D. Brown Institute of Mathematical Statistics, pp. 124–143.
-
- Agueh M, Carlier G, 2011. Barycenters in the wasserstein space. SIAM J. Math. Anal 43, 904–924.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

