Floquet-tailored Rydberg interactions

Abstract

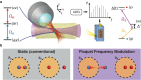
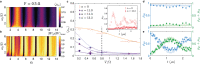
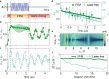
The Rydberg blockade is a key ingredient for entangling atoms in arrays. However, it requires atoms to be spaced well within the blockade radius, which limits the range of local quantum gates. Here we break this constraint using Floquet frequency modulation, with which we demonstrate Rydberg-blockade entanglement beyond the traditional blockade radius and show how the enlarged entanglement range improves qubit connectivity in a neutral atom array. Further, we find that the coherence of entangled states can be extended under Floquet frequency modulation. Finally, we realize Rydberg anti-blockade states for two sodium Rydberg atoms within the blockade radius. Such Rydberg anti-blockade states for atoms at close range enables the robust preparation of strongly-interacting, long-lived Rydberg states, yet their steady-state population cannot be achieved with only the conventional static drive. Our work transforms between the paradigmatic regimes of Rydberg blockade versus anti-blockade and paves the way for realizing more connected, coherent, and tunable neutral atom quantum processors with a single approach.

Fig. 1. Using Floquet frequency modulation to transform Rydberg interactions.

a Experiment setup for implementing FFM on two tweezer-trapped ²³Na atoms with counter-propagating Rydberg lasers at 589 nm (Ω₁) and 409 nm (Ω₂). The 589 nm Rydberg laser is frequency-modulated with an acousto-optic modulator (AOM) driven by an arbitrary waveform generator (AWG). b Transforming between the two regimes of interactions: Rydberg blockade (two entangled atoms depicted as blue/red spheres) versus anti-blockade (two red atoms). With the conventional static drive, the Rydberg blockade regime can only be accessed with the atoms positioned well within the blockade radius R_b, while atoms spaced farther than the blockade radius experience anti-blockade. The counter-intuitive regime of interactions can be exploited with Floquet frequency modulation, where atoms outside the static blockade radius experience Rydberg blockade and vice versa, as predicted by refs. ^,.

Fig. 2. Extended Rydberg blockade range.

a Calculated $∣ee⟩$ population, time averaged over 5 μs, and b calculated maximum $∣W⟩$ fidelities as a function of normalized modulation frequency ω₀/Ω and modulation index α. c Measured $∣ee⟩$ population, time-averaged over 2.5 μs, as a function of normalized interaction strength V/Ω for ω₀ = 3 Ω and different modulation indices {α}. Horizontal error bars are attributed to the position uncertainty of the atoms. Solid lines indicate the numerical modeling results for the corresponding α. (Inset) Population dynamics ρ_ee at V = 0.8 Ω. d, e Population dynamics for (left axis, blue) ρ_gg and (right axis, green) ρ_eg + ρ_ge, measured at V = 0.8 Ω and ω₀ = 3 Ω. The shaded curves reflect the results of Monte Carlo simulations. d Population trapping in $∣gg⟩$ is observed for α = 5.5, where J₀(α) ≈ 0. e At α = 6.9, the $∣W⟩$ state is generated with a calculated maximum fidelity of 0.77(5). In panels c–e, the displayed vertical error bar associated with each data point reflects the 1σ confidence interval.

Fig. 3. Dynamical stabilization of entangled states at the Bessel function zero α = 5.5 and at V = 8 Ω.

a Pulse sequence comprising an initial π pulse, 2 μs of FFM (ω₀ = 6 Ω), followed by static driving. b, c Observed population dynamics ρ_eg + ρ_ge b under the above FFM pulse sequence versus c under a continuous, resonant static drive. The solid lines account for the decoherence effects as modeled by Lindblad superoperators. The shaded bands depict Monte Carlo simulations that include the atom position uncertainty. d Comparison of $∣W⟩$ decay for (left axis, green) FFM versus (right axis, blue) a laser-free evolution. The FFM evolution yields a decay time of 14(5) μs whereas the laser-free evolution yields a decay time of 11(2) μs. Error bars in panels (b–d) depict the 1σ confidence interval. e Calculated IPR as a function of rescaled Doppler shift 10Δ_D/Ω and normalized modulation frequency ω₀/Ω. (White dashed line) At ω₀ = 7 Ω, the IPR is approximately 0 over an extended range of Doppler shifts, which is desired for robust dynamical stabilization of $∣W⟩$. f Calculated $∣W⟩$ fidelity for different Doppler shift widths after 20 μs of (green) FFM or (blue) laser-free evolution. Here the FFM parameters are ω₀ = 7 Ω, α = 5.5.

Fig. 4. Enhanced Rydberg anti-blockade dynamics at V = ω₀ = 6 Ω.

a Calculated $∣ee⟩$ population, time-averaged over 10 μs, as a function of normalized modulation frequency ω₀/Ω and modulation index α. The green and white dashed lines indicate positions at which J₀(α) = 0 and J₁(α) = 0, respectively. b The two-atom Rabi frequencies {Ω_a, Ω_b} depend strongly on the modulation index. (Green diamond) At α = 1.4, both Rabi frequencies have large values and can be used to access Rydberg anti-blockade states. c Measured population dynamics (top) ρ_ee, (middle) ρ_eg + ρ_ge, and (bottom) ρ_gg for α = 1.4, which are in good agreement with Monte Carlo simulations represented by shaded curves (in same color as data points). Error bars represent the 1σ confidence interval. (Brown shading) The FFM-induced anti-blockade population can be further increased with the help of ground-state cooling. The gray shading indicates the simulated ρ_ee achieved by FFM under both ground-state cooling and enhanced coherence times of 74 μs. In general, the FFM dynamics are faster than that with an off-resonant static drive (black dashed line), where Δ₀ = V/2. d Simulation of steady-state Rydberg anti-blockade, achieved by combining FFM with STIRAP. (Top) The modulation index α is smoothly varied from 2.4 to 0, such that the two-atom Rabi frequencies change in time despite holding Ω constant. (Bottom) Calculated population dynamics ρ_ee for the proposed STIRAP sequence. (Red line) In the absence of imperfections, ρ_ee can be as high as 0.98. (Gray line) With ground state cooling and enhanced coherence times of 74 μs, the mean steady-state population becomes ρ_ee = 0.85, with one standard deviation of the Monte Carlo sample distribution depicted as the half width of the light gray band.