Signature of quantum criticality in cuprates by charge density fluctuations

Abstract

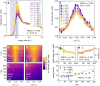
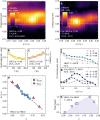
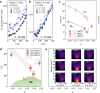
The universality of the strange metal phase in many quantum materials is often attributed to the presence of a quantum critical point (QCP), a zero-temperature phase transition ruled by quantum fluctuations. In cuprates, where superconductivity hinders direct QCP observation, indirect evidence comes from the identification of fluctuations compatible with the strange metal phase. Here we show that the recently discovered charge density fluctuations (CDF) possess the right properties to be associated to a quantum phase transition. Using resonant x-ray scattering, we studied the CDF in two families of cuprate superconductors across a wide doping range (up to p = 0.22). At p* ≈ 0.19, the putative QCP, the CDF intensity peaks, and the characteristic energy Δ is minimum, marking a wedge-shaped region in the phase diagram indicative of a quantum critical behavior, albeit with anomalies. These findings strengthen the role of charge order in explaining strange metal phenomenology and provide insights into high-temperature superconductivity.

Fig. 1. Charge density fluctuations in overdoped cuprates.

High resolution (ΔE = 38 meV) RIXS spectra have been measured on YBCO and Bi2212 (p ≈ 0.19) at several momenta along both the (H,0) and (H,H) directions, at T = 80 K and T = 200 K. a, b Intensity maps of the difference (H,0) – (H,H) taken at 80 K on YBCO and Bi2212. c Fit of a RIXS spectrum on Bi2212 at a representative momentum. The green, red, orange, blue Gaussians and the region below the gray dashed line represent respectively the pure elastic (mainly given by the specular peak centered at Γ = (0,0)), the CDF, the bond-stretching phonon modes, the bond-stretching overtone and the paramagnons. Additional details on the fit are provided in the Methods section. Given the position, intensity and width of the Gaussians, we have obtained, as a function of q along the (H,0) direction and at both temperatures, d the area of the elastic line, e the area of the CDF peak, and f the bond-stretching phonon dispersion. The error bars are estimated using the 95% confidence interval of the fit. In panel f the orange lines are guides to the eye while the gray line represents the phonon dispersion in absence of any softening, as measured in ref. . g–i Same as d–f, but on YBCO. In panel i, the gray line represents the phonon dispersion in absence of any softening, as measured in ref. .

Fig. 2. CDF energy from the T-dependence of the quasi-elastic spectral weight.

Medium resolution (ΔE = 62 meV) RIXS spectra have been measured on YBCO (p ≈ 0.185) at several momenta along both the (H,0) and (H,H) directions, in the temperature range between T = 20 K and T = 290 K. a RIXS spectra taken at a representative momentum as a function of the temperature. The vertical band represents the energy range, [−0.1, 0.035] eV, where the spectral intensity has been integrated to single out the CDF contribution. b, c The integrated intensity measured respectively along the (H,0) and (H,H) directions is shown as a contour plot as a function of the temperature. d, e Global fit of the curves presented in panels b and c, respectively along the (H,0) and (H,H) direction, achieved by modeling the CDF peak with the product of the Bose distribution function and of the imaginary part of the dynamical density fluctuation propagator (Eqs. (1) and (2)). Here, the experimental data are fitted considering ω₀ varying with temperature in the range 5–20 meV, $\overline{\mathrm{\omega }}$ = 45.55 meV, ν₀ = 1.26 eV(r.l.u.)⁻², γ = 1.6. f The CDF peak, given by the difference (H,0)-(H,H), is plotted at several temperatures. g, h The height and FWHM of the single Lorentzian profiles used to fit the data in panel f are presented as a function of the temperature. The error bars represent the 95% confidence interval of the Lorentzian fit. The solid line is a linear fit of the data. i The characteristic CDF energy $\mathrm{\Delta }$, extracted from the high resolution spectra by the energy position of the CDF Gaussians, and the frequency ω₀, determined from the medium resolution spectra by the FWHM of the CDF profiles, are plotted as a function of the temperature respectively as triangles and circles. Remarkably, the frequency ω₀ at q = q_CDF, as determined by the global fit (solid line), is in very good qualitative agreement with the experiment.

Fig. 3. Doping dependence of the charge density fluctuations in YBCO.

a High resolution RIXS map along the (H,0) direction taken at T = 20 K for a strongly underdoped (p = 0.06) YBCO. The map is presented after subtracting the fit of the pure elastic peak from the raw spectra. b, c Height and FWHM as a function of the temperature of the Lorentzian profiles used to fit the CDF peak. Here, the peak has been obtained from the difference (H,0) - (H,H) of the intensity of the medium resolution RIXS spectra, integrated within the energy range shown in Fig. 2a. The error bars represent the 95% confidence interval of the Lorentzian fit. The solid line is a linear fit of the data. d The H_CDF of the CDF peaks in the YBCO and Ca-YBCO samples we have measured is in agreement with the H_CDW doping dependence of CDW previously found in YBCO (see squares, taken from ref. ). The same linear trend is indeed also followed by the samples at p = 0.06 and p = 0.22, where no signature of charge order was previously detected. e High resolution RIXS map of the difference (H,0) – (H,H) taken at T = 60 K for an overdoped (p = 0.22) Ca-YBCO sample. f The integrated intensity at T ≈ 290 K is presented as a function of the momenta along the (H,0) direction for YBCO samples at different level of doping p. Curves are presented after a vertical translation, so to align the integrated intensities at the lowest and highest momentum values. g The CDF peak, determined by the difference (H,0) - (H,H), is shown at T ≈ 290 K for strongly underdoped (p = 0.06) YBCO, for a slightly overdoped (p = 0.185) YBCO, and for an overdoped (p = 0.22) Ca-YBCO thin film. For clarity, the weak, high-temperature CDF peaks are here presented after smoothing. h The height of the CDF peak, normalized to the maximum value measured at p ≈ 0.19, is plotted vs doping for the YBCO and Ca-YBCO. The violet region is a guide to the eye.

Fig. 4. Charge density fluctuations in the cuprate phase diagram.

a The integrated intensity measured on YBCO (p ≈ 0.06) is presented as a function of the temperature for several momenta along the (H,H) direction. For each momentum, the solid line represents the fit of the data assuming a Bose distribution function. b Same as previous panel, on YBCO (p ≈ 0.19). c The energies Ω, determined from the Bose fit on spectra measured along the (H,H) direction, are plotted together with the energies $\mathrm{\Delta }$, directly measured at q = q_CDF in the very high resolution spectra. Here and in the next panel we consider the $\mathrm{\Delta }$ value measured at the lowest temperature. The two NBCO samples are from Ref. . At any doping, Ω > $\mathrm{\Delta }$, as expected when moving away from q_CDF. As highlighted by the lines, which are guides to the eye, both energies increase when decreasing the doping, with a minimum at p = 0.19. d The temperatures corresponding to the energies $\mathrm{\Delta }$ are presented as a function of doping p as filled symbols. In the constructed cuprate phase diagram, we also show the temperature T_L, where the linear-in-T dependence of the resistance, signature of the strange metal behavior, is lost in YBCO and Bi2212^,,. e In the p-T phase diagram, we have depicted the CDF dispersion relation at three temperatures (T ≈ 20 K, T ≈ 100 K, T ≈ 300 K) and doping levels (p = 0.06, p = 0.19, p = 0.22), using the propagator of Eq. (2) and the energy values experimentally determined in this work.