Phase and sensitivity of receiver coils in magnetic resonance imaging
- PMID: 3796476
- PMCID: PMC2396267
- DOI: 10.1118/1.595967
Phase and sensitivity of receiver coils in magnetic resonance imaging
Abstract
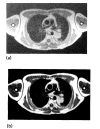
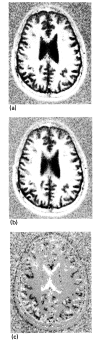
Receiver coil response is a major cause of nonuniformities in magnetic resonance images. The spatial dependence of the sensitivity and phase of single-saddle receiver coils has been investigated quantitatively by calculating the H1 field and comparing the results with measurements of a uniform phantom. Agreement between the measurements and calculations is excellent. A method is developed which corrects for both the nonuniform sensitivity and the phase shifts introduced by receiver coils.
Figures







Similar articles
-
Solenoid surface coils in magnetic resonance imaging.AJR Am J Roentgenol. 1986 Feb;146(2):409-12. doi: 10.2214/ajr.146.2.409. AJR Am J Roentgenol. 1986. PMID: 3484592
-
In vivo method for correcting transmit/receive nonuniformities with phased array coils.Magn Reson Med. 2005 Mar;53(3):666-74. doi: 10.1002/mrm.20377. Magn Reson Med. 2005. PMID: 15723397
-
MR spectroscopy using multi-ring surface coils.Magn Reson Med. 1999 Oct;42(4):655-64. doi: 10.1002/(sici)1522-2594(199910)42:4<655::aid-mrm6>3.0.co;2-d. Magn Reson Med. 1999. PMID: 10502753
-
Radiofrequency coils for magnetic resonance applications: theory, design, and evaluation.Crit Rev Biomed Eng. 2014;42(2):109-35. doi: 10.1615/critrevbiomedeng.2014011482. Crit Rev Biomed Eng. 2014. PMID: 25403875 Review.
-
Theory and application of array coils in MR spectroscopy.NMR Biomed. 1997 Dec;10(8):394-410. doi: 10.1002/(sici)1099-1492(199712)10:8<394::aid-nbm494>3.0.co;2-0. NMR Biomed. 1997. PMID: 9542737 Review.
Cited by
-
A new bias field correction method combining N3 and FCM for improved segmentation of breast density on MRI.Med Phys. 2011 Jan;38(1):5-14. doi: 10.1118/1.3519869. Med Phys. 2011. PMID: 21361169 Free PMC article.
-
A phased array coil for human cardiac imaging.Magn Reson Med. 1995 Jul;34(1):92-8. doi: 10.1002/mrm.1910340114. Magn Reson Med. 1995. PMID: 7674903 Free PMC article.
-
Recommendations of Choice of Head Coil and Prescan Normalize Filter Depend on Region of Interest and Task.Front Neurosci. 2021 Oct 29;15:735290. doi: 10.3389/fnins.2021.735290. eCollection 2021. Front Neurosci. 2021. PMID: 34776844 Free PMC article.
-
Phase-sensitive inversion recovery for detecting myocardial infarction using gadolinium-delayed hyperenhancement.Magn Reson Med. 2002 Feb;47(2):372-83. doi: 10.1002/mrm.10051. Magn Reson Med. 2002. PMID: 11810682 Free PMC article.
-
Medial femur T2 Z-scores predict the probability of knee structural worsening over 4-8 years: Data from the osteoarthritis initiative.J Magn Reson Imaging. 2017 Oct;46(4):1128-1136. doi: 10.1002/jmri.25662. Epub 2017 Feb 16. J Magn Reson Imaging. 2017. PMID: 28206712 Free PMC article.
References
-
- Bydder GM, Butsen PC, Harman RR, Gilderdale DJ, Young IR. J. Comput. Assist. Tomogr. 1985;9:413. - PubMed
-
- Glover GH, Hayes CE, Pelc NJ, Edelstein WA, Mueller OM, Hart HR, Hardy CJ, O’Donnell M, Barber WD. J. Magn. Reson. 1985;64:255.
-
- Leroy-Willig A, Darrasse L, Taquin J, Sauzadi M. Magn. Reson. Med. 1985;2:20. - PubMed
-
- Hinshaw WS, Gauss RC. Distributed phase rf coil. European Patent Application, Publ. No. 0047065. 1981.
-
- Hayes CE, Edelstein WA, Schenck JF, Mueller OW, Eash M. 1985; presented at the Soc. Magn. Reson. Med., Fourth Annual Meeting; London.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

