Student of Games: A unified learning algorithm for both perfect and imperfect information games

Abstract

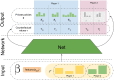
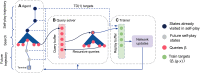
Games have a long history as benchmarks for progress in artificial intelligence. Approaches using search and learning produced strong performance across many perfect information games, and approaches using game-theoretic reasoning and learning demonstrated strong performance for specific imperfect information poker variants. We introduce Student of Games, a general-purpose algorithm that unifies previous approaches, combining guided search, self-play learning, and game-theoretic reasoning. Student of Games achieves strong empirical performance in large perfect and imperfect information games-an important step toward truly general algorithms for arbitrary environments. We prove that Student of Games is sound, converging to perfect play as available computation and approximation capacity increases. Student of Games reaches strong performance in chess and Go, beats the strongest openly available agent in heads-up no-limit Texas hold'em poker, and defeats the state-of-the-art agent in Scotland Yard, an imperfect information game that illustrates the value of guided search, learning, and game-theoretic reasoning.

Fig. 1.. An example structure of public belief state β = (s_pub, r).

s_pub translates to two sets of information states, one for player 1, ${\mathcal{S}}_1(s_{\mathrm{pub}})=\{{\overline{s}}_0,{\overline{s}}_1\}$, and one for player 2, 𝒮₂(s_pub) = {s₀, s₁, s₂}. Each information state includes different partitions of possible histories. Finally, r contains reach probabilities for information states for both players.

Fig. 2.. An example of depth-limited CFR solving using decomposition in a game with two specific subgames shown.

Standard CFR would require traversing all the subgames. Depth-limited CFR decomposes the solve into running down to depth d = 2 and using v = v_θ(β) to represent the second subgame’s values. On the downward pass, ranges r are formed from policy reach probabilities. Values are passed back up to tabulate accumulating regrets. Re-solving a subgame would require construction of an auxiliary game (36) (not shown).

Fig. 3.. Exploitability of SoG as a function of the number of training steps under different number of simulations of GT-CFR.

For both (A) Leduc poker and (B) Scotland Yard (glasses map), each line corresponds to a different evaluation condition, e.g., SoG(s, c) used at evaluation time. The ribbon shows minimum and maximum exploitability out of 50 seeded runs for each setup. The units of the y axis in Leduc poker are milli–big blinds per hand (mbb/h), which corresponds to one thousandth of a chip in Leduc. In Scotland Yard, the reward is either −1 (loss) or +1 (win). All networks were trained using a single training run of SoG(100,1), and the x values correspond to a network trained for the corresponding number of steps.

Fig. 4.. Scalability of SoG with increasing number of neural network evaluations compared to AlphaZero measured on relative Elo scale.

The x axis corresponds to the number of simulations in AlphaZero and s in SoG(s, c). Elo of SoG(s = 800, c) was set to be 0. In chess (A), c = 10 for all runs, with varying s ∈ {800,2400,7200,21600,64800}. In Go (B), we graph SoG using (s, c) ∈ {(800,1), (2000,10), (4000,10), (8000,10), (16000,16).}

Fig. 5.. Win rate of SoG(400,1) against PimBot with varying simulations.

Two thousand matches were played for each data point, with roles swapped for half of the matches. Note that the x axis has logarithmic scale. The ribbon shows 95% confidence interval.

Fig. 6.. A counterfactual value-and-policy network (CVPN).

Each query, β, to the network includes beliefs r and an encoding of s_pub to get the counterfactual values v for both players and policies p for the acting player in each information state s_i ∈ s_pub(h), producing outputs f_θ. Since players may have different actions spaces (as in, e.g., Scotland Yard), there are two sets of policy outputs: one for each player, and p refers to the one for the acting player at s_pub only (depicted as player 1 in this diagram by graying out player 2’s policy output).

Fig. 7.. Overview of the phases in one iteration of GT-CFR.

The regret update phase propagates beliefs down the tree, obtains counterfactual values from the CVPN at leaf nodes (or from the environment at terminals), and passes back counterfactual values to apply the CFR update. The expansion phase simulates a trajectory from the root to a leaf, adding public states to the tree. In this case, the trajectory starts in the public belief state s_pub by sampling the information state s₀. After that, the sampled action a₀ leads to the information state $s_0^0$ in public state $s_{\mathrm{pub}}^0$, and finally, the action a₁ leads to a new public state that is added to the tree.

Fig. 8.. SoG training process.

Actors collect data via sound self-play and trainers run separately over a distributed network. (A) Each search produces a number of CVPN queries with input β. (B) Queries are added to a query buffer and subsequently solved by a solver that studies the situation more closely via another invocation of GT-CFR. During solving, new recursive queries might be added back to the query buffer; separately, the network is (C) trained on minibatches sampled from the replay buffer to predict values and policy targets computed by the solver.