Kondo screening in a Majorana metal

Abstract

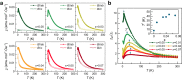
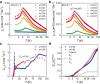
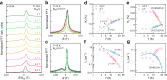
Kondo impurities provide a nontrivial probe to unravel the character of the excitations of a quantum spin liquid. In the S = 1/2 Kitaev model on the honeycomb lattice, Kondo impurities embedded in the spin-liquid host can be screened by itinerant Majorana fermions via gauge-flux binding. Here, we report experimental signatures of metallic-like Kondo screening at intermediate temperatures in the Kitaev honeycomb material α-RuCl₃ with dilute Cr³⁺ (S = 3/2) impurities. The static magnetic susceptibility, the muon Knight shift, and the muon spin-relaxation rate all feature logarithmic divergences, a hallmark of a metallic Kondo effect. Concurrently, the linear coefficient of the magnetic specific heat is large in the same temperature regime, indicating the presence of a host Majorana metal. This observation opens new avenues for exploring uncharted Kondo physics in insulating quantum magnets.

Fig. 1. Schematic sketch of gauge-flux-driven Kondo screening, x-T phase diagram, and fractionalized excitations of α-Ru_1−xCr_xCl₃.

a (Top) A Kitaev paramagnetic state consists of coherently propagating Majorana fermions (black dots) and thermally populated π-fluxes (W_p = −1) out of the frozen Z₂ gauge fluxes (incarnadine hexagons; W_p = +1). (Bottom) Spin−1/2 impurities coupled strongly to individual host spins (blue spheres) engender impurity plaquettes (W_I = −1; gray polygons) by a gauge flux in the three adjacent plaquettes. In addition, distant magnetic impurities can interact via long-range interactions (orange arrows). b T–x phase diagram of α-Ru_1−xCr_xCl₃ (x = 0–0.07). The characteristic temperatures T_K^onset, T_K^end, and T_N are determined from the dc magnetic susceptibility, specific heat, and μSR measurements. The band edge energy D is evaluated from the logarithmic fits to the magnetic susceptibility. The black dashed curve is a guide to the eye. AFM stands for antiferromagnetically ordered phase. c As-measured Raman spectra at T = 5 K. The color shadings denote the broad magnetic continuum. The inset plots the normalized intensity of the magnetic continuum as function of the concentration of the Cr³⁺(S = 3/2) impurities.

Fig. 2. Static magnetic susceptibility and magnetic anisotropy as a function of Cr content.

a Temperature dependence of dc magnetic susceptibility χ(T) of α-Ru_1−xCr_xCl₃ (x = 0–0.07) measured in an applied field of B = 0.1 T along the ab plane (full symbols) and the c-axis (open symbols). The out-of-plane χ_c(T) shows a drastic increase with increasing x, rendering the magnetism of α-Ru_1−xCr_xCl₃ isotropic. b Temperature and composition dependence of the magnetic anisotropy χ_ab/χ_c of α-Ru_1−xCr_xCl₃ measured in an applied field of B = 0.1 T. An XY-like magnetic anisotropy is systematically reduced with increasing Cr³⁺ concentration. The downward arrows indicate the broad maximum temperature T^* in χ_ac/χ_c. The inset plots T^* versus x.

Fig. 3. Thermodynamic signatures of Kondo screening.

a, b Temperature dependence of the static magnetic susceptibility χ_c(T) and the pristine-subtracted Δχ_c(T) = χ_c(T) –χ_c(T;x = 0) for α-Ru_1−xCr_xCl₃ (x = 0.01–0.07) in an applied field of B//c = 0.1 T. The solid lines are fittings to logarithmic divergence Δχ(T)~ln(D/T), where D is the band edge energy. c Comparison of the T-dependent magnetic specific heat C_m(T) between α-Ru_1−xCr_xCl₃ (x = 0.04) and the pristine material (x = 0). C_m(T) is obtained by subtracting a lattice contribution from the total specific heat (Supplementary Fig. 12). The solid lines indicate a T-linear dependence of C_m(T). The error bars represent one standard deviation of the three repeated specific-heat measurements. d Normalized magnetic entropy S_m/S_m^theory as a function of temperature evaluated by integrating C_m(T)/T in a semi-log scale. S_m^theory is Rln2 and 0.96Rln2 + 0.04Rln4 for x = 0.00 and 0.04, respectively. The solid and dashed lines denote a fit using three phenomenological functions (“Methods”).

Fig. 4. High transverse-field μSR data of α-Ru_1−xCr_xCl₃ (x = 0.04).

a Normalized FFT amplitudes of hTF-μSR in applied fields of B_ext//c = 0.2–3 T at T = 15 K. The data are vertically shifted for clarity. b, c Magnified views of normalized FFT amplitudes at B_ext = 0.5 and 3 T. The black solid lines denote the total fitting lines that are a sum of two Lorentzian damped cosines (yellow and green lines). d, e Temperature dependence of the muon Knight shift for the fast (K_f) and slow (K_s) relaxing components in applied fields of B_ext//c = 0.5 and 3 T. K_f(T) is described by power-law behaviors K_f ~ T⁻ⁿ (dashed lines), which deviates below T_N2 = 12 K, while K_s(T) exhibits a logarithmic dependence K_s~ln(D/T) (solid lines) predicted for a singlet vortex case above 10 K. Error bars represent one standard deviation. f, g Muon spin-relaxation rates for the fast (λ_f) and slow (λ_s) component as a function of temperature on a double logarithmic scale. λ_f(T) displays a power-law down to T_N2 (dashed lines), similar to K_f. On the other hand, λ_s(T) at B_ext = 3 T is well described by a logarithmic dependence λ_s ~ 1/T₁ ~ T[ln(D/T)]² (solid lines). Error bars of the muon Knight shift and the relaxation rat represent one standard deviation of the fit parameters.