A laboratory and simulation platform to integrate individual life history traits and population dynamics
- PMID: 37981946
- PMCID: PMC10655596
- DOI: 10.1038/s43588-022-00190-8
A laboratory and simulation platform to integrate individual life history traits and population dynamics
Abstract
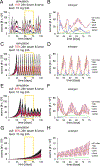
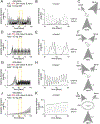
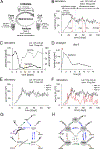
Understanding populations is important because they are a fundamental level of biological organization. Individual traits such as aging and lifespan interact in complex ways to determine birth and death and thereby influence population dynamics. However, we lack a deep understanding of the relationships between individual traits and population dynamics. To address this challenge, we established a laboratory population using the model organism C. elegans and an individual-based computational simulation informed by measurements of real worms. The simulation realistically models individual worms and the behavior of the laboratory population. To elucidate the role of aging in population dynamics, we analyzed old age as a cause of death and showed, using computer simulations, that it was influenced by maximum lifespan, rate of adult culling, and progeny number/food stability. Notably, populations displayed a tipping point for aging as the primary cause of adult death. Our work establishes a conceptual framework that could be used for better understanding why certain animals die of old age in the wild.
Conflict of interest statement
Declaration of Interest The authors declare no competing interests.
Figures

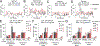
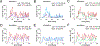
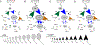

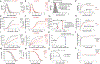




References
-
- Medawar P An unsolved problem of Biology (1952).
-
- Promislow DEL Senescence in natural populations of mammals: A comparative study. Evolution (N. Y) 48, 1869–1887 (1991). - PubMed
-
- Gaillard JM & Lemaître JF An integrative view of senescence in nature. Funct. Ecol 34, 4–16 (2020).
Grants and funding
LinkOut - more resources
Full Text Sources

