Isometric Hamming embeddings of weighted graphs
- PMID: 37982050
- PMCID: PMC10653646
- DOI: 10.1016/j.dam.2023.02.005
Isometric Hamming embeddings of weighted graphs
Abstract
A mapping from the vertex set of one graph to another graph is an isometric embedding if the shortest path distance between any two vertices in equals the distance between their images in . Here, we consider isometric embeddings of a weighted graph into unweighted Hamming graphs, called Hamming embeddings, when satisfies the property that every edge is a shortest path between its endpoints. Using a Cartesian product decomposition of called its canonical isometric representation, we show that every Hamming embedding of may be partitioned into a canonical partition, whose parts provide Hamming embeddings for each factor of the canonical isometric representation of . This implies that permits a Hamming embedding if and only if each factor of its canonical isometric representation is Hamming embeddable. This result extends prior work on unweighted graphs that showed that an unweighted graph permits a Hamming embedding if and only if each factor is a complete graph. When a graph has nontrivial isometric representation, determining whether has a Hamming embedding can be simplified to checking embeddability of two or more smaller graphs.
Keywords: Graph embeddings; Graph factorization; Hamming graphs; Isometric embeddings; Metric spaces; Weighted graphs.
Conflict of interest statement
Declaration of competing interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures
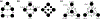
References
-
- Avis D, Hypermetric spaces and the Hamming cone, Canad. J. Math. 33 (4) (1981) 795–802.
-
- Bandelt H-J, Retracts of hypercubes, J. Graph Theory 8 (4) (1984) 501–510.
-
- Björner A, Edelman PH, Ziegler GM, Hyperplane arrangements with a lattice of regions, Discrete Comput. Geom. 5 (3) (1990) 263–288.
Grants and funding
LinkOut - more resources
Full Text Sources
