How Cell-Penetrating Peptides Behave Differently from Pore-Forming Peptides: Structure and Stability of Induced Transmembrane Pores
- PMID: 37989570
- PMCID: PMC11870675
- DOI: 10.1021/jacs.3c08014
How Cell-Penetrating Peptides Behave Differently from Pore-Forming Peptides: Structure and Stability of Induced Transmembrane Pores
Abstract
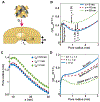
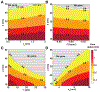
Peptide-induced transmembrane pore formation is commonplace in biology. Examples of transmembrane pores include pores formed by antimicrobial peptides (AMPs) and cell-penetrating peptides (CPPs) in bacterial membranes and eukaryotic membranes, respectively. In general, however, transmembrane pore formation depends on peptide sequences, lipid compositions, and intensive thermodynamic variables and is difficult to observe directly under realistic solution conditions, with structures that are challenging to measure directly. In contrast, the structure and phase behavior of peptide-lipid systems are relatively straightforward to map out experimentally for a broad range of conditions. Cubic phases are often observed in systems involving pore-forming peptides; however, it is not clear how the structural tendency to induce negative Gaussian curvature (NGC) in such phases is quantitatively related to the geometry of biological pores. Here, we leverage the theory of anisotropic inclusions and devise a facile method to estimate transmembrane pore sizes from geometric parameters of cubic phases measured from small-angle X-ray scattering (SAXS) and show that such estimates compare well with known pore sizes. Moreover, our model suggests that although AMPs can induce stable transmembrane pores for membranes with a broad range of conditions, pores formed by CPPs are highly labile, consistent with atomistic simulations.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
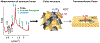
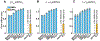

Update of
-
How cell penetrating peptides behave differently from pore forming peptides: structure and stability of induced transmembrane pores.bioRxiv [Preprint]. 2023 Jul 27:2023.07.26.550729. doi: 10.1101/2023.07.26.550729. bioRxiv. 2023. Update in: J Am Chem Soc. 2023 Dec 6;145(48):26095-26105. doi: 10.1021/jacs.3c08014. PMID: 37546874 Free PMC article. Updated. Preprint.
Similar articles
-
How cell penetrating peptides behave differently from pore forming peptides: structure and stability of induced transmembrane pores.bioRxiv [Preprint]. 2023 Jul 27:2023.07.26.550729. doi: 10.1101/2023.07.26.550729. bioRxiv. 2023. Update in: J Am Chem Soc. 2023 Dec 6;145(48):26095-26105. doi: 10.1021/jacs.3c08014. PMID: 37546874 Free PMC article. Updated. Preprint.
-
The importance of membrane defects-lessons from simulations.Acc Chem Res. 2014 Aug 19;47(8):2244-51. doi: 10.1021/ar4002729. Epub 2014 Jun 3. Acc Chem Res. 2014. PMID: 24892900
-
Thermodynamics of cell-penetrating HIV1 TAT peptide insertion into PC/PS/CHOL model bilayers through transmembrane pores: the roles of cholesterol and anionic lipids.Soft Matter. 2016 Aug 10;12(32):6716-27. doi: 10.1039/c5sm01696g. Soft Matter. 2016. PMID: 27435187
-
Estimation of pore dimensions in lipid membranes induced by peptides and other biomolecules: A review.Biochim Biophys Acta Biomembr. 2021 Apr 1;1863(4):183551. doi: 10.1016/j.bbamem.2021.183551. Epub 2021 Jan 16. Biochim Biophys Acta Biomembr. 2021. PMID: 33465367 Review.
-
Challenge to overcome current limitations of cell-penetrating peptides.Biochim Biophys Acta Proteins Proteom. 2021 Apr;1869(4):140604. doi: 10.1016/j.bbapap.2021.140604. Epub 2021 Jan 14. Biochim Biophys Acta Proteins Proteom. 2021. PMID: 33453413 Review.
Cited by
-
Chemokines Kill Bacteria by Binding Anionic Phospholipids without Triggering Antimicrobial Resistance.bioRxiv [Preprint]. 2024 Jul 25:2024.07.25.604863. doi: 10.1101/2024.07.25.604863. bioRxiv. 2024. Update in: Sci Adv. 2025 Jun 6;11(23):eads2675. doi: 10.1126/sciadv.ads2675. PMID: 39091850 Free PMC article. Updated. Preprint.
-
Dynamin-like Proteins Combine Mechano-constriction and Membrane Remodeling to Enable Two-Step Mitochondrial Fission via a "Snap-through" Instability.J Am Chem Soc. 2025 Jul 16;147(28):24258-24274. doi: 10.1021/jacs.5c06352. Epub 2025 Jul 8. J Am Chem Soc. 2025. PMID: 40626390 Free PMC article.
-
Dynamins combine mechano-constriction and membrane remodeling to enable two-step mitochondrial fission via a 'snap-through' instability.bioRxiv [Preprint]. 2024 Aug 20:2024.08.19.608723. doi: 10.1101/2024.08.19.608723. bioRxiv. 2024. Update in: J Am Chem Soc. 2025 Jul 16;147(28):24258-24274. doi: 10.1021/jacs.5c06352. PMID: 39229060 Free PMC article. Updated. Preprint.
-
Effective cell membrane tension protects red blood cells against malaria invasion.PLoS Comput Biol. 2023 Dec 4;19(12):e1011694. doi: 10.1371/journal.pcbi.1011694. eCollection 2023 Dec. PLoS Comput Biol. 2023. PMID: 38048346 Free PMC article.
-
Chemokines kill bacteria without triggering antimicrobial resistance by binding anionic phospholipids.Sci Adv. 2025 Jun 6;11(23):eads2675. doi: 10.1126/sciadv.ads2675. Epub 2025 Jun 6. Sci Adv. 2025. PMID: 40479071 Free PMC article.
References
-
- Zasloff M Antimicrobial Peptides of Multicellular Organisms. Nature 2002, 415 (6870), 389–395. - PubMed
-
- Brogden KA Antimicrobial Peptides: Pore Formers or Metabolic Inhibitors in Bacteria? Nat. Rev. Microbiol 2005, 3 (3), 238–250. - PubMed
-
- Yu Y; Vroman JA; Bae SC; Granick S Vesicle Budding Induced by a Pore-Forming Peptide. J. Am. Chem. Soc 2010, 132 (1), 195–201. - PubMed
-
- Shai Y Mechanism of the Binding, Insertion and Destabilization of Phospholipid Bilayer Membranes by α-Helical Antimicrobial and Cell Non-Selective Membrane-Lytic Peptides. Biochim. Biophys. Acta, Biomembr 1999, 1462 (1), 55–70. - PubMed
-
- Youle RJ; Strasser A The BCL-2 Protein Family: Opposing Activities That Mediate Cell Death. Nat. Rev. Mol. Cell Biol 2008, 9 (1), 47–59. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

