Bayesian Optimization-Based Inverse Finite Element Analysis for Atrioventricular Heart Valves

Abstract

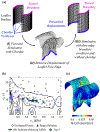
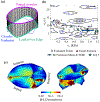
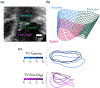
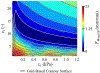
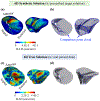
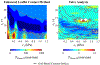
Inverse finite element analysis (iFEA) of the atrioventricular heart valves (AHVs) can provide insights into the in-vivo valvular function, such as in-vivo tissue strains; however, there are several limitations in the current state-of-the-art that iFEA has not been widely employed to predict the in-vivo, patient-specific AHV leaflet mechanical responses. In this exploratory study, we propose the use of Bayesian optimization (BO) to study the AHV functional behaviors in-vivo. We analyzed the efficacy of Bayesian optimization to estimate the isotropic Lee-Sacks material coefficients in three benchmark problems: (i) an inflation test, (ii) a simplified leaflet contact model, and (iii) an idealized AHV model. Then, we applied the developed BO-iFEA framework to predict the leaflet properties for a patient-specific tricuspid valve under a congenital heart defect condition. We found that the BO could accurately construct the objective function surface compared to the one from a [Formula: see text] grid search analysis. Additionally, in all cases the proposed BO-iFEA framework yielded material parameter predictions with average element errors less than 0.02 mm/mm (normalized by the simulation-specific characteristic length). Nonetheless, the solutions were not unique due to the presence of a long-valley minima region in the objective function surfaces. Parameter sets along this valley can yield functionally equivalent outcomes (i.e., closing behavior) and are typically observed in the inverse analysis or parameter estimation for the nonlinear mechanical responses of the AHV. In this study, our key contributions include: (i) a first-of-its-kind demonstration of the BO method used for the AHV iFEA; and (ii) the evaluation of a candidate AHV in-silico modeling approach wherein the chordae could be substituted with equivalent displacement boundary conditions, rendering the better iFEA convergence and a smoother objective surface.

Keywords: Constitutive model parameters; Heart valve biomechanics; In-silico modeling; Statistics-based modeling.

Fig. 1.

(a) Geometry of the inflation test (Test Case 1). (b) Element-by-element bidirectional local distance (B-LD) errors depicted for the optimal solution. (c) Surface of the mean Gaussian process (GP) from Bayesian optimization. (d) Contour plot of the mean Gaussian process and the mean and standard error of the mean (SEM) of the top 5% of the BO-evaluated solutions (numbers in blue indicate the value of $ℱ$ normalized by the characteristic length (2 mm) for each contour level, in mm/mm). (e) Optimization history showcasing the value of $ℱ$ normalized by the characteristic length (2 mm).

Fig. 2.

(a) Schematic of the simplified model for two leaflets in contact. (b) Elementwise bidirectional local distance (B-LD) errors for the optimal BO solution normalized by the characteristic length (4.03 mm). (c) Mean Gaussian process surface from the BO procedure.

Fig. 3.

(a) Illustration of the process for developing the leaflet contact optimization Test Case 3 with prescribed leaflet free edge displacements (Test Case 2). (b) Contour surface of the objective function when using free-edge leaflet displacements and the mean and standard error of the mean (SEM) of the top 5% of the BO-evaluated solutions. Note the contour surface is generated from the mean Gaussian process model and the numbers in blue indicate the value of $ℱ$ for each contour level normalized by the characteristic length (4.03 mm). (c) Element-by-element bidirectional local distance (B-LD) measures for the optimal solution.

Fig. 4.

(a) Tricuspid valve model used in the forward simulation of the target (synthetic) solution (Test Case 3). (b) Contour surface of the objective function and the mean and standard error of the mean (SEM) of the top 5% of the BO-evaluated solutions (numbers in blue indicate the value of $ℱ$ for each contour level normalized by the characteristic length (79.28 mm)). (c) Element-by-element bidirectional local distance (B-LD) measures for the optimal solution (left: superior view; right: isometric view).

Fig. 5.

(a) Illustration of image segmentation of the patient-speciifc echocardiogram to retrieve the TV annulus, free edge, and leaflet point clouds. (b) Generated finite element mesh for the three TV leaflets. (c) Dynamic displacement conditions prescribed for the TV annulus and leaflet free edge (t₁ = right ventricle minimum volume and t₄ = end diastole).

Fig. 6.

Comparison of the Gaussian process model approximation of the objective function surface (shaded contour map) against the contour map generated from a uniform $20\times 20$ grid search (white solid lines) normalized by the characteristic length (2 mm).

Fig. 7.

(a) Top-down and isometric views of the element-wise bidirectional local distance (B-LD) errors normalized by the characteristic length (56.46 mm) and (b) qualitative comparisons with the leaflet point cloud for the optimized TV surface with the 6D synthetic and (c, d) true solutions. Note that for improved visualization a denser finite element mesh was generated than what was used in the real optimization.

Fig. 8.

Comparison of the Gaussian process model approximation of the objective function (shaded contour map) with the contour map generated from a uniform $20\times 20$ grid search (solid lines) for (a) the proposed leaflet simulation method (Section 2.2.3) normalized by the characteristic length (4.03 mm) and (b) the full valve analysis test case (Section 2.2.4) normalized by the characteristic length (79.28 mm).