Response of a three-species cyclic ecosystem to a short-lived elevation of death rate

Abstract

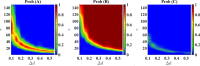
A balanced ecosystem with coexisting constituent species is often perturbed by different natural events that persist only for a finite duration of time. What becomes important is whether, in the aftermath, the ecosystem recovers its balance or not. Here we study the fate of an ecosystem by monitoring the dynamics of a particular species that encounters a sudden increase in death rate. For exploration of the fate of the species, we use Monte-Carlo simulation on a three-species cyclic rock-paper-scissor model. The density of the affected (by perturbation) species is found to drop exponentially immediately after the pulse is applied. In spite of showing this exponential decay as a short-time behavior, there exists a region in parameter space where this species surprisingly remains as a single survivor, wiping out the other two which had not been directly affected by the perturbation. Numerical simulations using stochastic differential equations of the species give consistency to our results.

Figure 1

Schematic diagram of the death-pulse applied on species A. The elevated death rate remains active for the time duration $\tau$.

Figure 2

Real time dynamics of the densities of A (red line), B (blue dashed line), and C (green dot-dashed line) for different initial configurations and different $\tau$, all having $\mathrm{\Delta }d=0.2$: Three rows (I, II, III) are for three different initial configurations, and five columns (a - e) are for five different values of $\tau$: $15,25,35,45,55$.

Figure 3

Probabilities of occurring (A, 0, 0) or (0, B, 0) or (0, 0, C) as a final state on $\mathrm{\Delta }d-\tau$ plane. Large value of pulse and pulse duration steers the system such a way that only B survives (see red color in middle panel). Note that, for all cases, if the pulse or pulse duration is significantly high, the C species can never outperform the species A or B (right panel).

Figure 4

Probabilities of occurring (A, 0, 0) or (0, B, 0) or (0, 0, C) as a final state on $\mathrm{\Delta }d-\tau$ plane obtained through numerical solution of stochastic differential equations. The results are almost consistent with the Monte-Carlo simulation (Fig. 3).

Figure 5

Dynamics inside the pulse: $ln{\rho }_a$ vs time for $\tau =15,25,35$ (marked by vertical dotted-dashed lines) having $\mathrm{\Delta }d=0.1,0.2,0.3$ for left, middle and right panel respectively and starting from the same initial configuration. The black dashed line shows the curve for exponential decay of the form ${\rho }_a^{0}exp(-\mathrm{\Delta }dt)$, where ${\rho }_a^0=0.21$.