Cell-Matrix Elastocapillary Interactions Drive Pressure-based Wetting of Cell Aggregates
- PMID: 38009085
- PMCID: PMC10673637
- DOI: 10.1103/physrevx.12.031027
Cell-Matrix Elastocapillary Interactions Drive Pressure-based Wetting of Cell Aggregates
Abstract
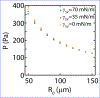
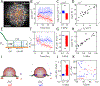
Cell-matrix interfacial energies and the energies of matrix deformations may be comparable on cellular length-scales, yet how capillary effects influence tis sue shape and motion are unknown. In this work, we induce wetting (spreading and migration) of cell aggregates, as models of active droplets onto adhesive substrates of varying elasticity and correlate the dynamics of wetting to the balance of interfacial tensions. Upon wetting rigid substrates, cell-substrate tension drives outward expansion of the monolayer. By contrast, upon wetting compliant substrates, cell substrate tension is attenuated and aggregate capillary forces contribute to internal pressures that drive expansion. Thus, we show by experiments, data-driven modeling and computational simulations that myosin-driven 'active elasto-capillary' effects enable adaptation of wetting mechanisms to substrate rigidity and introduce a novel, pressure-based mechanism for guiding collective cell motion.
Figures

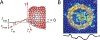







Similar articles
-
Active wetting of epithelial tissues: modeling considerations.Eur Biophys J. 2023 Feb;52(1-2):1-15. doi: 10.1007/s00249-022-01625-w. Epub 2023 Jan 2. Eur Biophys J. 2023. PMID: 36593348 Review.
-
How cells flow in the spreading of cellular aggregates.Proc Natl Acad Sci U S A. 2014 Jun 3;111(22):8055-60. doi: 10.1073/pnas.1323788111. Epub 2014 May 16. Proc Natl Acad Sci U S A. 2014. PMID: 24835175 Free PMC article.
-
Interplay between substrate rigidity and tissue fluidity regulates cell monolayer spreading.Soft Matter. 2022 Oct 19;18(40):7877-7886. doi: 10.1039/d2sm00757f. Soft Matter. 2022. PMID: 36205535 Free PMC article.
-
Confinement induces internal flows in adherent cell aggregates.J R Soc Interface. 2024 May;21(214):20240105. doi: 10.1098/rsif.2024.0105. Epub 2024 May 22. J R Soc Interface. 2024. PMID: 38774959 Free PMC article.
-
Adhesion of bubbles and drops to solid surfaces, and anisotropic surface tensions studied by capillary meniscus dynamometry.Adv Colloid Interface Sci. 2016 Jul;233:223-239. doi: 10.1016/j.cis.2015.06.003. Epub 2015 Jun 19. Adv Colloid Interface Sci. 2016. PMID: 26143156 Review.
Cited by
-
An EpCAM/Trop2 mechanostat differentially regulates collective behaviour of human carcinoma cells.EMBO J. 2025 Jan;44(1):75-106. doi: 10.1038/s44318-024-00309-9. Epub 2024 Nov 21. EMBO J. 2025. PMID: 39572744 Free PMC article.
-
Patterning and folding of intestinal villi by active mesenchymal dewetting.Cell. 2024 Jun 6;187(12):3072-3089.e20. doi: 10.1016/j.cell.2024.04.039. Epub 2024 May 22. Cell. 2024. PMID: 38781967 Free PMC article.
-
Elastocapillary effects determine early matrix deformation by glioblastoma cell spheroids.APL Bioeng. 2024 May 3;8(2):026109. doi: 10.1063/5.0191765. eCollection 2024 Jun. APL Bioeng. 2024. PMID: 38706957 Free PMC article.
-
Patterning and folding of intestinal villi by active mesenchymal dewetting.bioRxiv [Preprint]. 2023 Aug 15:2023.06.25.546328. doi: 10.1101/2023.06.25.546328. bioRxiv. 2023. Update in: Cell. 2024 Jun 6;187(12):3072-3089.e20. doi: 10.1016/j.cell.2024.04.039. PMID: 37425793 Free PMC article. Updated. Preprint.
-
Using Biosensors to Study Organoids, Spheroids and Organs-on-a-Chip: A Mechanobiology Perspective.Biosensors (Basel). 2023 Sep 24;13(10):905. doi: 10.3390/bios13100905. Biosensors (Basel). 2023. PMID: 37887098 Free PMC article. Review.
References
Grants and funding
LinkOut - more resources
Full Text Sources
