Inequality-Constrained 3D Morphable Face Model Fitting
- PMID: 38015704
- PMCID: PMC10823595
- DOI: 10.1109/TPAMI.2023.3334948
Inequality-Constrained 3D Morphable Face Model Fitting
Abstract
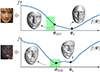
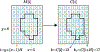
3D morphable model (3DMM) fitting on 2D data is traditionally done via unconstrained optimization with regularization terms to ensure that the result is a plausible face shape and is consistent with a set of 2D landmarks. This paper presents inequality-constrained 3DMM fitting as the first alternative to regularization in optimization-based 3DMM fitting. Inequality constraints on the 3DMM's shape coefficients ensure face-like shapes without modifying the objective function for smoothness, thus allowing for more flexibility to capture person-specific shape details. Moreover, inequality constraints on landmarks increase robustness in a way that does not require per-image tuning. We show that the proposed method stands out with its ability to estimate person-specific face shapes by jointly fitting a 3DMM to multiple frames of a person. Further, when used with a robust objective function, namely gradient correlation, the method can work "in-the-wild" even with a 3DMM constructed from controlled data. Lastly, we show how to use the log-barrier method to efficiently implement the method. To our knowledge, we present the first 3DMM fitting framework that requires no learning yet is accurate, robust, and efficient. The absence of learning enables a generic solution that allows flexibility in the input image size, interchangeable morphable models, and incorporation of camera matrix.
Figures


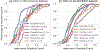

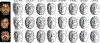
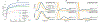
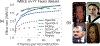

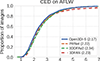


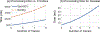

References
-
- Bagdanov AD, Del Bimbo A, and Masi I, “The florence 2d/3d hybrid face dataset,” in ACM Workshop on Human Gesture and Behavior Understanding, 2011, pp. 79–80.
-
- Bai Z, Cui Z, Liu X, and Tan P, “Riggable 3d face reconstruction via in-network optimization,” in CVPR, 2021, pp. 6216–6225.
-
- Baker S and Matthews I, “Lucas-Kanade 20 years on: A unifying framework,” IJCV, vol. 56, no. 3, pp. 221–255, 2004.
-
- Bas A, Smith WA, Bolkart T, and Wuhrer S, “Fitting a 3D morphable model to edges: A comparison between hard and soft correspondences,” in ACCV, 2016, pp. 377–391.
-
- Blanz V and Vetter T, “A morphable model for the synthesis of 3D faces,” in Proceedings of the Conference on Computer Graphics and Interactive Techniques. ACM Press/Addison-Wesley Publishing Co., 1999, pp. 187–194.

