Chaos in a bacterial stress response

Abstract

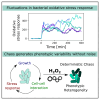
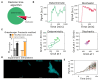
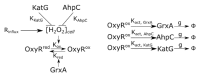
Cellular responses to environmental changes are often highly heterogeneous and exhibit seemingly random dynamics. The astonishing insight of chaos theory is that such unpredictable patterns can, in principle, arise without the need for any random processes, i.e., purely deterministically without noise. However, while chaos is well understood in mathematics and physics, its role in cell biology remains unclear because the complexity and noisiness of biological systems make testing difficult. Here, we show that chaos explains the heterogeneous response of Escherichia coli cells to oxidative stress. We developed a theoretical model of the gene expression dynamics and demonstrate that chaotic behavior arises from rapid molecular feedbacks that are coupled with cell growth dynamics and cell-cell interactions. Based on theoretical predictions, we then designed single-cell experiments to show we can shift gene expression from periodic oscillations to chaos on demand. Our work suggests that chaotic gene regulation can be employed by cell populations to generate strong and variable responses to changing environments.

Keywords: bacterial stress response; chaos; gene regulation; oxidative stress; phenotypic heterogeneity; single-cell analysis.

Graphical abstract

Figure 1. Modeling the oxidative stress response in bacterial populations

(A) Environmental stress, such as H₂O₂ exposure, induces heterogeneous responses in bacterial populations, which could be caused by stochastic or deterministic mechanisms. (B) H₂O₂ affects cell growth rates (G) and triggers an intracellular stress response (S) that creates stressor gradients by cell-cell interactions (I). S-G-I feedback modulates H₂O₂ concentration in space and time, both outside and inside the bacteria ([H₂O₂]_external, [H₂O₂]_cell, respectively). (C) Schematic of the core OxyR gene regulatory circuit corresponding to the stress response component of the model. It predicts the expression dynamics of proteins that scavenge intracellular H₂O₂ (KatG, AhpCF) and control OxyR oxidation status (GrxA). Model output illustrated for constant [H₂O₂]_external exposure from 0 min. (D) The growth model describes the inhibition of cell elongation by H₂O₂. In turn, the growth dynamics feed into the stress response model by determining the dilution rate of enzymes. Top: cell elongation rate as a function of intracellular H₂O₂. Bottom: exponential growth and division cycles of a single cell without H₂O₂ treatment. (E) Cell-cell interactions are described by a reaction-diffusion model where intracellular scavenging of H₂O₂ creates a stress gradient from the edge to the interior of a cell population. Changes in the number and arrangement of cells in the population are determined by the growth model. See also Figure S1.

Figure 2. The model predicts chaos in the stress response

(A) Oxidative stress response fluctuations in individual “mother cells” at the base of a one-dimensional population with “barrier cells” positioned closer to the H₂O₂ source. The model produces seemingly random dynamics of GrxA protein expression level during continuous H₂O₂ treatment from t = 0 min. The curves represent three independent simulation runs, starting with unsynchronized cells at random points in the cell cycles. (B) Stress response fluctuations diverge greatly over time, even if the differences in initial conditions are very small: here shown by the GrxA dynamics for 3 mother cells that differ very slightly in their initial stage of the cell cycle (2.5·10⁻⁴% and 5·10⁻⁴ % length differences). (C) (Left) Representative GrxA dynamics for a mother cell with continuous treatment at different H₂O₂ concentrations (80, 140, and 260 μM). (Right) Histogram of counts of extrema detected for 3 mother cells for different H₂O₂ concentrations. (D) Phase diagrams for the GrxA dynamics of the mother cells presented in (C), displaying bistable (80 mM) and multistable periodic oscillations (140 μM) and chaotic fluctuations (260 μM). (E) Bifurcation plot of the GrxA extrema values over a range of H₂O₂ concentrations (n = 3 simulations per concentration). Vertical lines represent example traces in (C) and (D). (F) A positive Lyapunov exponent (λ) shows chaotic divergence from initial conditions, computed for GrxA dynamics at different H₂O₂ concentrations. Individual points represent single mother cells, with red dots for chaos (λ>0) and black dots for periodicity (λ ≤ 0). Blue line and shaded region show mean ± SD of n = 3 cells simulated per H₂O₂ concentration. (G) The autocorrelation function (ACF) distinguishes periodic and chaotic response fluctuations. Mean of ACF for GrxA of mother cells decreases steeply for chaotic traces under high H₂O₂ treatment (1.7 mM, purple) and shows regular peaks for periodic traces under low H₂O₂ treatment (140 μM, orange) (n = 3 simulations). See also Figure S2 and Video S1.

Figure 3. Chaos emerges in a general model of stress responses in cell populations

(A) Uptake of toxins reduces cell growth rates (G) and triggers an intracellular stress response (S) that creates toxin gradients by cell-cell interactions (I). S-G-I feedback modulates toxin concentration in space and time, both outside and inside the bacteria ([Toxin]_external, [Toxin]_cell respectively). (B) Schematic of a generic stress response in which exposure to a toxin induces the expression of a detoxifying enzyme with rate K_activation that removes toxin with rate K_cat. (C) Model output illustrates the expression dynamics of the enzyme (maroon) and the intracellular toxin concentration (yellow) for constant external toxin exposure from t = 0 min without S-G-I feedback. (D) A positive Lyapunov exponent (λ) shows chaotic divergence from initial conditions, computed for enzyme expression dynamics over a range of toxin concentrations (n = 3 simulations per toxin concentration). Higher external toxin concentrations lead to chaos. (E) Phase diagrams for the enzyme expression dynamics of a mother cell at toxin concentrations marked by vertical lines in (D), displaying periodic oscillations and chaotic fluctuations. (F) Higher K_cat of the enzyme increases chaotic behavior. Lyapunov exponent for enzyme expression dynamics over a range of K_cat values. (G) Phase diagrams for the enzyme expression dynamics of a mother cell at K_cat values marked in (F), displaying periodic oscillations and chaotic fluctuations. (H) Higher expression rate K_activation of the enzyme increases chaotic behavior. Lyapunov exponent for enzyme expression dynamics over a range of K_activation values. (I) Phase diagrams for the enzyme expression dynamics of a mother cell at K_activation values marked in (H), displaying periodic oscillations and chaotic fluctuations.

Figure 4. Experiments on the oxidative stress response in E. coli reveal a good fit with the modeling predictions

(A) Top: model simulation snapshot of GrxA expression after 90 min of 100 μM H₂O₂ treatment. Bottom: snapshot of experiment with E. coli cells growing in a “mother machine” expressing PgrxA-SCFP3 after 90 min of 100 μM H₂O₂ treatment. Scale bar, 10 μm. (B and C) Model simulation predictions and experimental data for mean GrxA expression (left) and mean cell elongation rates (right) under constant 100 μM H₂O₂ treatment from t = 0 min for cells at different positions in growth trench (n = 100 simulated trenches and 3 experimental repeats). (D) PgrxA-SCFP3 dynamics of individual cells diverge greatly over time under constant 100 μM H₂O₂ treatment from t = 0 min in experiments (5 representative mother cells shown). (E) The steep decay of the autocorrelation function (ACF) of the response fluctuations is consistent with chaos. Mean of ACF for PgrxA-SCFP3 of mother cells with 100 μM H₂O₂ treatment (blue, 3 experimental repeats). ACF for individual cell traces shown in black (n = 100). See also Figure S3 and Video S2.

Figure 5. Measurements of stress response dynamics in E. coli are consistent with chaos

(A) Decision tree algorithm by Toker et al. suggests that most mother cells in experiments display deterministic and chaotic response dynamics under 100 μM H₂O₂ treatment. Pie-chart indicates the fraction of dead (red) and alive (green/black) mother cells detected as having stochastic (black/red) or deterministic (green) dynamics under 100 μM H₂O₂ (n = 3,581 cells, 3 experimental repeats). (B) PgrxA traces (top) and their phase diagrams (bottom) for representative mother cell traces treated with 100 μM H₂O₂ treatment from t = 0 min, which are classified as deterministic (green) or stochastic (red). (C) Bar plots show mean and standard deviation of maximal correlation dimension for experimental (black) and model (orange) GrxA traces of mother cell with (dark) or without shuffling (light) under 100 μM H₂O₂ treatment, as computed by the Grassberger-Procaccia method. Random shuffling was performed as a control to remove temporal relation between data points. The low correlation dimension is consistent with determinism in experiments and simulations. (D) Stress response dynamics of cells growing in a colony are consistent with chaos. Snapshots of PgrxA-SCFP3 expression with 1 μM H₂O₂ treatment from t = 0 min show cell-cell variability (scale bar, 10 μM). (E) Single-cell trajectories from the colony experiment in (D) are consistent with chaotic divergence of stress response dynamics. See also Figures S3, S4, S5, and S6 and Video S3.

Figure 6. Predicted perturbations make or break chaos in experiments

Model predicts that chaos no longer occurs for reduced strength of either of the model components (growth, G; interactions, I; or response, S). Mean and standard deviation of Lyapunov exponent (λ) show a transition from deterministic (λ ≤ 0) to chaotic (λ > 0) GrxA dynamics in simulations of cells with increasing (A) growth rates, (B) population size, and (C) H₂O₂ concentration. Experimental designs to test model predictions by changing (A) growth media, (B) trench lengths, and (C) H₂O₂ concentrations. Snapshots (scale bars, 10 μM) of PgrxA-SCFP3 90 min after start of treatment for cells growing in (A) M9 glycerol (slow growth, top) or M9 glucose + 10% LB (fast growth, bottom) in 25-μm trenches treated with 100 μM H₂O₂. (B) M9 glucose + 10% LB in 10-μm (2–4 cells per trench, top) or 25-μm (5–7 cells per trench, bottom) trenches treated with 25 μM H₂O₂. (C) M9 glucose + 10% LB in 10-μm trenches treated with 25 μM H₂O₂ (top) or 100 μM H₂O₂ (bottom). Autocorrelation analysis demonstrates the predicted transitions from periodic to chaotic dynamics in experiments. ACF curves of PgrxA-SCFP3 dynamics show characteristic peaks for periodic oscillations (black); these peaks are absent for chaotic dynamics (teal) in the case of (A) growth rate perturbation (1,806 and 1,991 cells, respectively; n ≥ 3 repeats), (B) population size perturbation (1,003 and 1,440 cells, respectively; n ≥ 3 repeats), and (C) H₂O₂ concentration perturbation (1,003 and 1,361 cells, respectively; n ≥ 3 repeats). (d) Bar plots show mean and standard deviation of maximal correlation dimension for GrxA traces of mother cells in experimental conditions shown in (A), (B), and (C) resulting in chaos (teal), or periodicity (black), as obtained from the Grassberger-Procaccia method. (E) The periods of non-chaotic oscillations correlate with cell cycle duration (interdivision time) over a range of growth rates in simulations and experiments. Mean and standard deviation of interdivision time and the time of the first ACF peak for simulated GrxA dynamics (left, n = 3 simulations per condition) and experiments (right) with 100 μM H₂O₂ in M9 glycerol in 25-μm trenches (black), 50 μM H₂O₂ in M9 glucose in 10-μm trenches (dark blue), and 25 μM H₂O₂ in M9 glucose + 10% LB in 10-μm trenches (light blue) (966, 397, and 661 cells, respectively; n ≥ 3 repeats). See also Figures S2 and S6 and Videos S4–S6.