Thermal Oscillations of Nanobubbles

Abstract

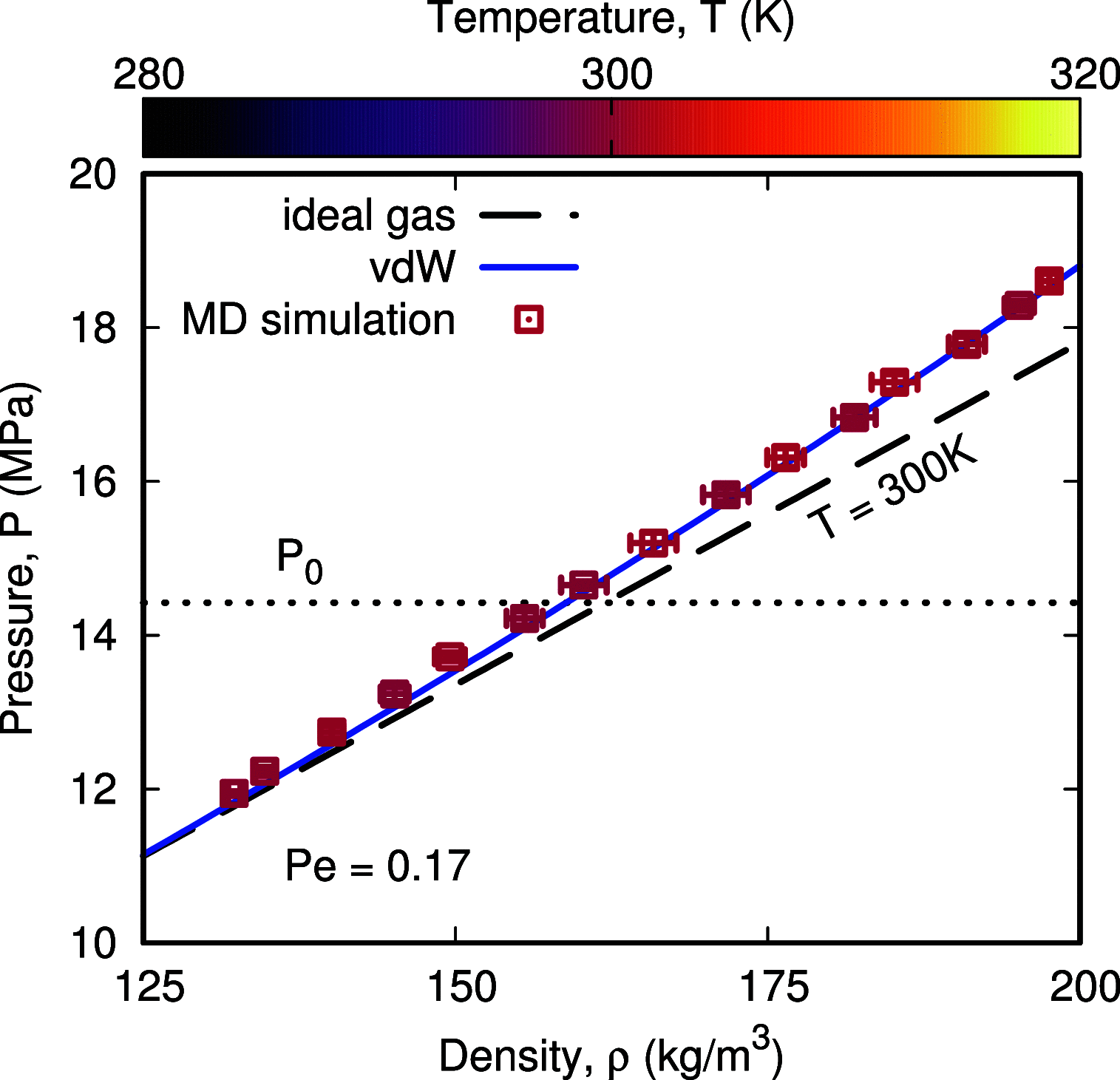
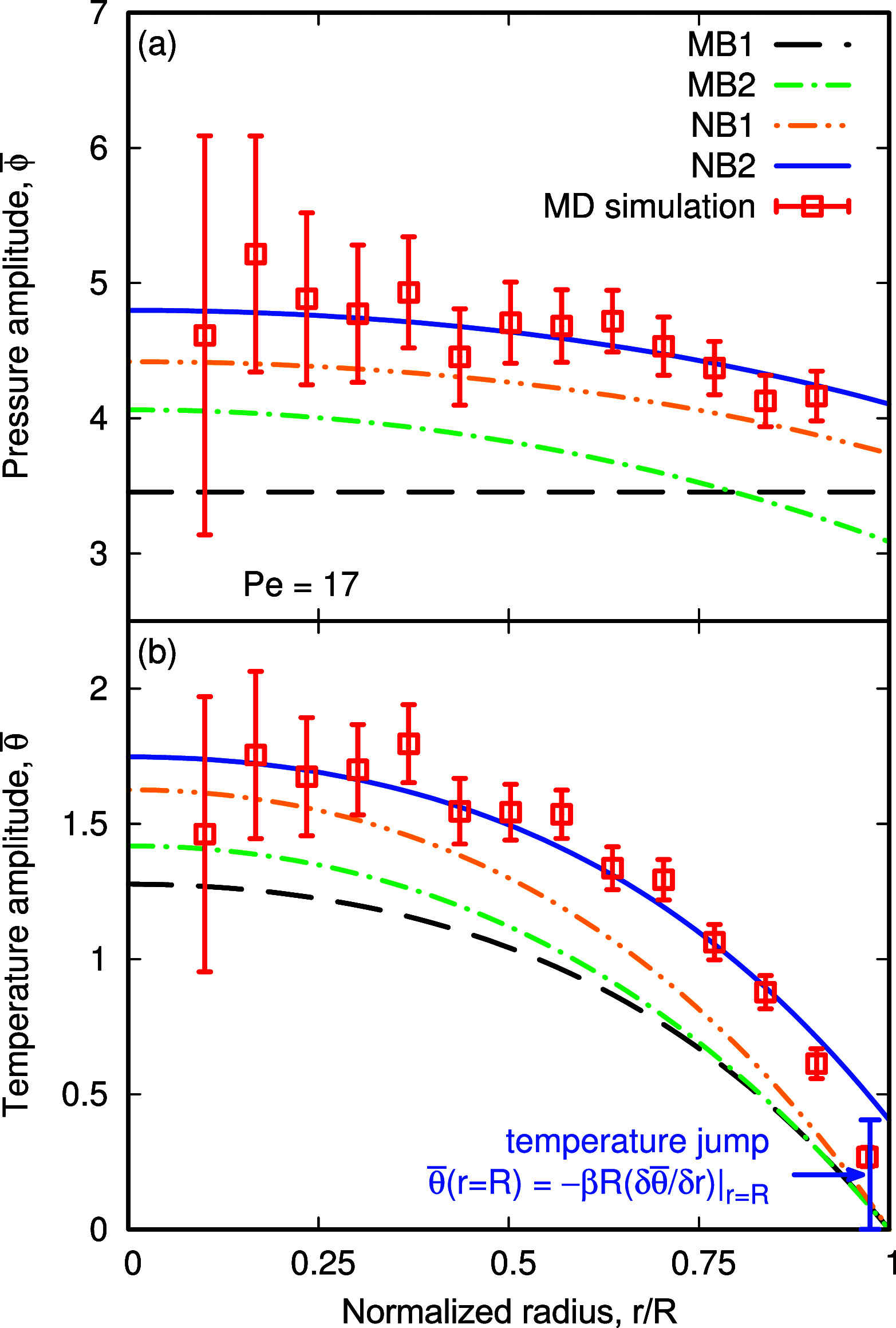
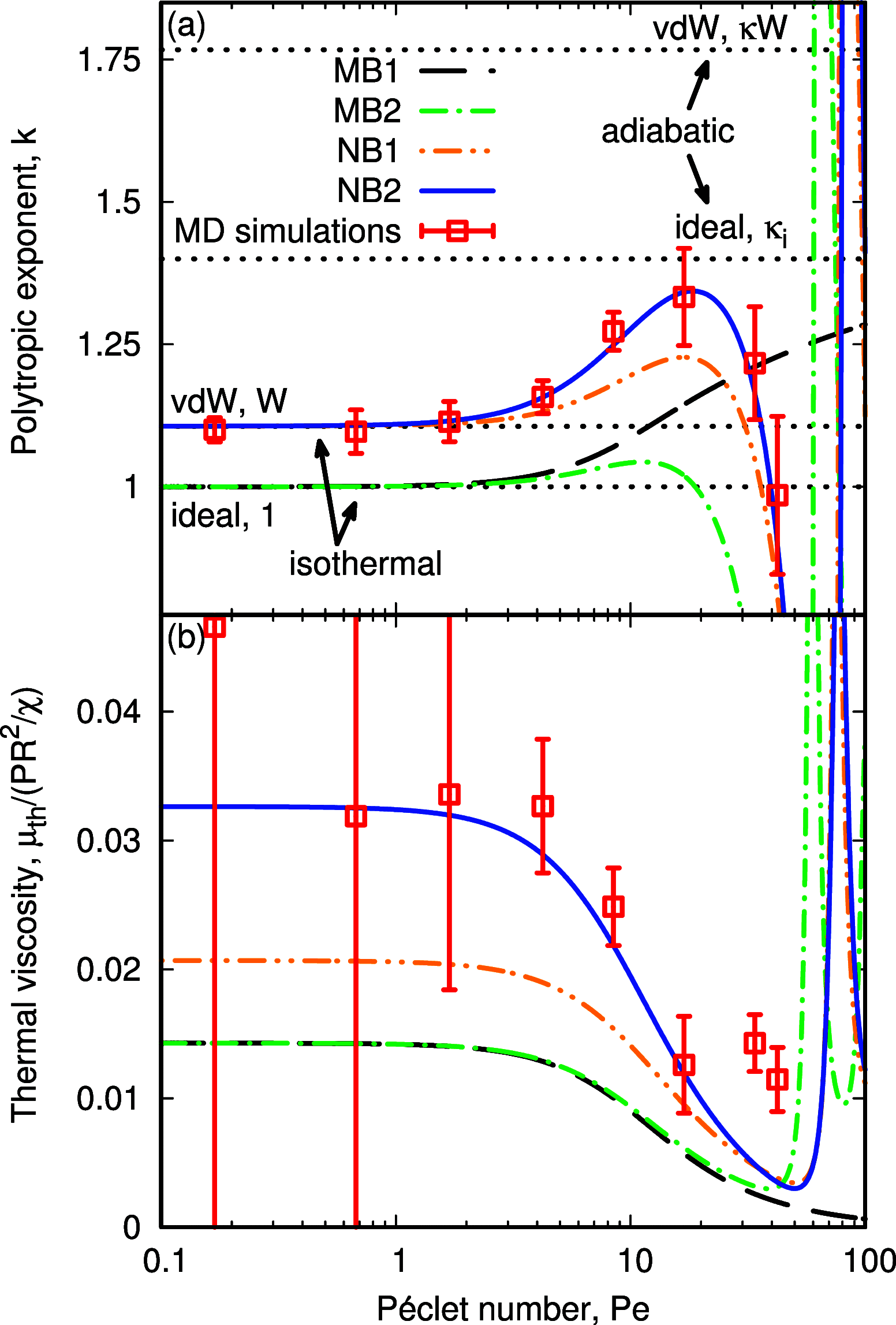
Nanobubble cavitation is advancing technologies in enhanced wastewater treatment, cancer therapy and diagnosis, and microfluidic cleaning. Current macroscale models predict that nanobubble oscillations should be isothermal, yet recent studies suggest that they are adiabatic with an associated increase in natural frequency, which becomes challenging when characterizing nanobubble sizes using ultrasound in experiments. We derive a new theoretical model that considers the nonideal nature of the nanobubble's internal gas phase and nonequilibrium effects, by employing the van der Waals (vdW) equation of state and implementing a temperature jump term at the liquid-gas interface, respectively, finding excellent agreement with molecular dynamics (MD) simulations. Our results reveal how adiabatic behavior could be erroneously interpreted when analyzing the thermal response of the gas using the commonly employed polytropic process and explain instead how nanobubble oscillations are physically closer to their isothermal limit.

Keywords: cavitation; nanobubbles; nonequilibrium gas; nonideal gas; oscillations; thermodynamics.

Figure 1

Schematic showing nanobubbles being employed in a microfluidic channel for cavitation applications. Insets show enhanced views of (a) nanobubbles entering microfluidic networks, that microbubbles are too large to reach, (b) the high-speed jets released during the final collapse stage, which have been proposed for the novel cavitation applications shown, and (c) nanobubbles being stimulated to oscillate using high-frequency ultrasound, such as in ultrasound contrast agents. (d) Molecular dynamics (MD) simulation setup for our nanobubble simulations, forced to oscillate using a vibrating piston, shown with a sliced view. The oxygen atoms are shown in red, hydrogen atoms in white, nitrogen atoms in cyan, and wall/piston atoms in gray. The inset shows an orthographic view of the three-dimensional domain, with some water molecules in the dashed box removed for clarity. Variation in (e) nanobubble radius R, (f) mean internal gas pressure P, and (g) mean internal gas temperature T, with time t, for the ω = 25 rad/ns oscillation case.

Figure 2

Variation in the nanobubble’s gas pressure P (and temperature T, shown in color) with density ρ, for the Pe = 0.17 oscillation case. MD simulation results are compared with the vdW equation of state in eq 2, and the ideal gas law P = ρk_BT/M_g, both at T = 300 K. The equilibrium gas pressure P₀ is also shown as a dotted line.

Figure 3

Radial variations of (a) pressure ϕ̅ and (b) temperature θ̅, nondimensional amplitudes in the oscillating nanobubble, for the Pe = 17 case. The temperature jump θ̅(r = R) at the liquid–gas interface is shown. The model cases, and their key assumptions, are summarized in Table 1.

Figure 4

Variation in (a) polytropic exponent k and (b) nondimensional thermal viscosity μ_th/(PR²/χ) with Péclet number Pe. The dotted lines in (a) show the limits for isothermal and adiabatic expansion for an ideal gas, k = 1 and k = κ_i = 1.4, respectively, and the vdW gas, k = W ≈ 1.11 and k = κW ≈ 1.77, respectively. The model cases, and their key assumptions, are summarized in Table 1.

Figure 5

Variation in (a) coefficients β, D, and (inset) W and κW, representing the polytropic limits for isothermal and adiabatic expansion, respectively, (b) polytropic exponent k, and (c) thermal viscosity μ_th (normalized by PR²/χ), with equilibrium radius R, when evaluated at the bubble’s natural frequency ω_n. The legend in (b) also applies to (c). The model cases, and their key assumptions, are summarized in Table 1.