Exploiting Locality in Full Configuration Interaction Quantum Monte Carlo for Fast Excitation Generation

Abstract

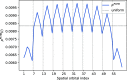
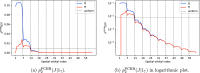
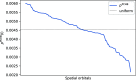
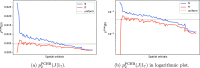
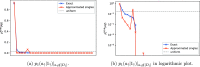
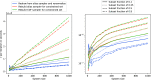
In this paper, we propose an improved excitation generation algorithm for the full configuration interaction quantum Monte Carlo method, which is particularly effective in systems described by localized orbitals. The method is an extension of the precomputed heat-bath strategy of Holmes et al., with more effective sampling of double excitations and a novel approach for nonuniform sampling of single excitations. We demonstrate the effectiveness of the algorithm for a chain of 30 hydrogen atoms with atom-localized orbitals, a stack of benzene molecules, and an Fe(II)-porphyrin model complex, whereby we show an overall efficiency gain by a factor of two to four, as measured by variance reduction per wall-clock time.

Figure 1

PCHB probability of the first particle p₂^PCHB(I) for a double excitation in a stack of 10 benzene molecules. The orbitals are ordered by fragment, and the vertical dotted lines separate MOs of different benzene molecules. Since α and β electrons have the same probability, assuming RHF-type orbitals, we could use the spatial orbital index. The horizontal dashed line gives the probability of the corresponding unconstrained uniform distribution p₂^uni(I) as reference. The value is obtained as 1/n_orb = 1/120 = 8.3 × 10^–3.

Figure 2

PCHB probability of the second particle after having picked an α electron in the first spatial orbital p₂^PCHB(J|1_↑) for a double excitation in a stack of 10 benzene molecules. The orbitals are sorted by fragment, and the vertical dotted lines separate MOs of different benzene molecules. We again use spatial orbital indices. The blue line represents an opposite spin p₂^PCHB(j_↓|1_↑), while the orange line represents a parallel spin p₂^PCHB(j_↑|1_↑) for the second electron. The right figure is a logarithmic version of the left one. The horizontal dashed line gives the probability of the corresponding unconstrained uniform distribution p₂^uni(J|1_↑) as the reference. The value is obtained as 1/n_orb = 1/120 = 8.3 × 10^–3.

Figure 3

PCHB probability of the first particle p₂^PCHB(I) for a double excitation in the N₂ dimer. The orbitals are sorted by probability. Since α and β electrons have the same probability, assuming RHF-type orbitals, we could use the spatial orbital index. The horizontal dashed line gives the probability of the corresponding unconstrained uniform distribution p₂^uni(I) as reference. The value is obtained as 1/n_orb = 1/220 = 4.5 × 10^–3.

Figure 4

PCHB probability of the second particle after having picked an α electron in the first spatial orbital p₂^PCHB(J|1_↑) for double excitation in the N₂ dimer. We use again spatial orbital indices, which are sorted by joint spatial probability, i.e., p₂^PCHB(j_α|1_↑) + p₂^PCHB(j_β|1_↑). The blue line represents an opposite spin p₂^PCHB(j_↓|1_↑), while the orange line represents a parallel spin p₂^PCHB(j_↑|1_↑) for the second electron. The right figure is a logarithmic version of the left one. The horizontal dashed line gives the probability of the corresponding unconstrained uniform distribution p₂^uni(J|1_↑) as reference. The value is obtained as 1/n_orb = 1/220 = 4.5 × 10^–3.

Figure 5

Sampling time for drawing from a constrained subset that contains half of the elements of the total system size using two different algorithms: redrawing method (blue line, algorithm 3) and rebuilding an alias table for the constrained subset (orange line). The right figure is a logarithmic version of the left one.

Figure 6

PCHB probability of the hole in a single excitation after having picked an α electron in the first spatial orbital, p₁^PCHB(a_↑|1_↑), on a stack of 10 benzene molecules. The blue line shows the exact probability (eq 20) assuming that the starting determinant |D_i⟩ = |2, 2, 2, 0, 0, 0; 2, ···⟩ is given by doubly occupying all π-orbitals and keeping all π*-orbitals empty for each benzene molecule. The orange line shows the approximated PCHB probabilities for single excitations (eq 23). Only unoccupied α spin–orbitals, i.e., allowed holes, are considered. The orbital indices are sorted by decreasing exact probability (blue line). (b) Logarithmic scale of (a). The horizontal dashed line gives the probability of the corresponding unconstrained uniform distribution p₁^uni(a_↑|1_↑)|_{a↑∉|Di⟩} as reference. The value is obtained from the inverse of the number of empty α-orbitals 1/(n_orb^↑ – N_e^↑) = 1/30 = 3.3 × 10^–2.

Figure 7

Stack of 10 benzene molecules at a distance of 3.0 Å.

Figure 8

Example of a GASCI wave function.

Figure 9

Sampling times of the alias method with and without the optional sorting step in the initialization (compare algorithm 2) against the system size n. The dotted lines are purely the sampling times, while the solid lines include the sampling and construction times.

Figure 10

Sampling times for drawing from a constrained subset. The colors denote the algorithm: blue uses redrawing (algorithm 3) orange and green rebuild an alias and CDF sampler for the constrained subset. The line style denotes the size of the subset measured as a fraction of the number of elements.