A robophysical model of spacetime dynamics

Abstract

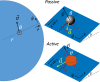
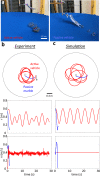
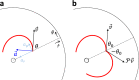
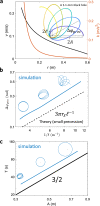
Systems consisting of spheres rolling on elastic membranes have been used to introduce a core conceptual idea of General Relativity: how curvature guides the movement of matter. However, such schemes cannot accurately represent relativistic dynamics in the laboratory because of the dominance of dissipation and external gravitational fields. Here we demonstrate that an "active" object (a wheeled robot), which moves in a straight line on level ground and can alter its speed depending on the curvature of the deformable terrain it moves on, can exactly capture dynamics in curved relativistic spacetimes. Via the systematic study of the robot's dynamics in the radial and orbital directions, we develop a mapping of the emergent trajectories of a wheeled vehicle on a spandex membrane to the motion in a curved spacetime. Our mapping demonstrates how the driven robot's dynamics mix space and time in a metric, and shows how active particles do not necessarily follow geodesics in the real space but instead follow geodesics in a fiducial spacetime. The mapping further reveals how parameters such as the membrane elasticity and instantaneous speed allow the programming of a desired spacetime, such as the Schwarzschild metric near a non-rotating blackhole. Our mapping and framework facilitate creation of a robophysical analog to a general relativistic system in the laboratory at low cost that can provide insights into active matter in deformable environments and robot exploration in complex landscapes.

Figure 1

A passive object (a marble) versus an active object (a robot) on a deformable membrane. While a passive marble is only subjected to friction and Earth’s gravity that leads to energy dissipation as $\overrightarrow{F}·\overrightarrow{v}\propto \overrightarrow{a}·\overrightarrow{v}<0$, an active object with an additional drive force can maintain steady-state motion with prescribed speed as $\overrightarrow{a}·\overrightarrow{v}=0$.

Figure 2

Trajectories of active and passive objects on an elastic membrane. (a) Sample perspective views of an active vehicle and a passive marble moving on a Spandex membrane. The time interval between two consecutive snapshots is 0.17 s. (b) The experimental trajectories, radius evolution, and speed evolution of the active (red) and the passive (blue) objects with the same mass (150 g) started from the same initial position and velocity on the same membrane. See the supplementary movie S1 for videos. (c) The simulation counterparts of (b).

Figure 3

Dynamics of the active vehicle. (a) The acceleration of an active vehicle is perpendicular to its velocity $\overrightarrow{v}$. (b) A non-chiral vehicle with a mirror-reflected initial velocity $\mathcal{P}\overrightarrow{v}$ will produce a mirror-reflected trajectory.

Figure 4

Creating orbits in Schwarzschild spacetime with a speed varying particle. (a) The speed and membrane elasticity’s dependence on radius to create a Schwarzschild blackhole with $r_s=3.1$ mm. The inset shows a precessing orbit with $A=0.3$ m using this prescription. (b) Precession angle $|\mathrm{\Delta }{\phi }_{\text{prec}}|$ as a function of inverse latus rectum. (c) The relation between the orbital period, T, and the semi-major-axis, A, follows Kepler’s third law as $T\propto A^{3/2}$. Insets in (b) and (c) show the trajectories around the data points. See the supplementary movieS1 for continuous evolution of the orbits.

Figure 5

Proposed scheme to create a spacetime with a non-diagonal metric. A controlled deformation (e.g., a tilted slab) rotating about the central axis shown in (A) could plausibly induce an asymmetric dependence on heading $\theta$ for the acceleration magnitude in blue instead of the symmetric counterpart in red. The spacetime metric resulting from this proposed setup would have a non-diagonal component $g_{t\varphi }$.

Figure 6

An experiment to probe the effective friction.

Figure 7

Orbits around the horizon ($r_s=3.1$ mm). As the initial radius gets closer to the event horizon shown in dashed line, the orbit approaches the blackhole and eventually is captured by the singularity at $r=r_s$. Using the method described earlier to integrate orbits outside the horizon, the orbit inside the horizon starts to show intriguing repulsion as predicted by.