Deep kinematic inference affords efficient and scalable control of bodily movements

Abstract

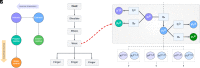
Performing goal-directed movements requires mapping goals from extrinsic (workspace-relative) to intrinsic (body-relative) coordinates and then to motor signals. Mainstream approaches based on optimal control realize the mappings by minimizing cost functions, which is computationally demanding. Instead, active inference uses generative models to produce sensory predictions, which allows a cheaper inversion to the motor signals. However, devising generative models to control complex kinematic chains like the human body is challenging. We introduce an active inference architecture that affords a simple but effective mapping from extrinsic to intrinsic coordinates via inference and easily scales up to drive complex kinematic chains. Rich goals can be specified in both intrinsic and extrinsic coordinates using attractive or repulsive forces. The proposed model reproduces sophisticated bodily movements and paves the way for computationally efficient and biologically plausible control of actuated systems.

Keywords: active inference; kinematics; motor control; neurocomputational modeling; predictive coding.

Fig. 1.

Generative models for deep kinematic inference. (A) The Intrinsic–Extrinsic (IE) generative model. The two hidden states are intrinsic and extrinsic coordinates, each with its own dynamics. The proprioceptive generative model extracts joint angles from the intrinsic belief, which are used for both posture inference and movement. At the same time, the exteroceptive model produces a visual prediction (in the simulations reported below, it is approximated by directly using the absolute position of the hand). Inverse kinematics is performed by inference, via backpropagation of extrinsic prediction errors. On the other hand, inverse dynamics from proprioceptive predictions to motor control signals is realized through reflex arcs. (B) The deep hierarchical generative model that extends the IE model. The deep model is exemplified for the control of a kinematic plant composed of seven blocks arranged hierarchically, from head to fingers (note that the bottom level is branched, as there are three fingers). Here, the highest (head) level only encodes an extrinsic offset, namely, the initial position and orientation of the origin’s reference frame. (C) Factor graph of a single level of the deep hierarchical model. Each block $j$ has the same structure as the kinematic generative model shown in Panel A, but with slight differences. In short, intrinsic beliefs ${\mathit{\mu }}_i^{(j)}$ and extrinsic beliefs ${\mathit{\mu }}_e^{(j)}$ are linked by a generative kinematic model ${\mathit{g}}_e$, and they encode information about a single kinematic level. They generate proprioceptive predictions ${\mathit{p}}_p^{(j)}$ and visual predictions ${\mathit{p}}_v^{(j)}$ only at their specific level. Intrinsic and extrinsic beliefs have their own dynamics, encoded in the functions ${\mathit{f}}_i^{(j)}$ and ${\mathit{f}}_e^{(j)}$, which predict future trajectories and are used for goal-directed behavior. Finally, the extrinsic belief at each level $j$ acts as a prior for the level below $j+1$.

Fig. 2.

Results. (A) Simulation setup: a 4R robotic arm with realistic joint limits reaching a static target (red circle). The trajectory of each joint is shown with blue lines. (B) Comparison between the deep kinematic model (deep), the simpler IE model (IE), and two standard active inference controllers based on Jacobian transpose (transp) and pseudoinverse (pinv). The blue and red bars denote the performance of the models during perceptual inference and reaching, respectively. Note that to better probe the model’s ability to perform perceptual inference, we only allow the model to use visual observations, but not proprioceptive observations during this phase (however, the model can still use proprioceptive observations for reaching). (C) Evolution over time of the difference between true and estimated end effector positions (blue line), and between true and estimated lengths of the body segments (green line), aggregated over 1,000 trials during inference only. The dashed gray line represents the minimum distance defining a successful inference.

Fig. 3.

Deep inference. Comparison between hierarchical models with increasing DoF (here, kinematic depth). Inference (Top) and reach (Bottom) simulations.

Fig. 4.

Applications. Track and avoid (A), maintain orientation (B), perform circular trajectory (C), avoid with a full human body (D), reach multiple targets with a full human body (E), and with a more complex kinematic tree (F). The trajectories in the first panel represent the hand-obstacle distance (red line), the hand-target distance (green line), and the minimum distance that the target is considered to be reached (dotted blue line). Instead, the trajectories in the next two panels show the absolute orientation of every joint (in particular, the purple line is the orientation of the hand). More information about the specific tasks and other applications can be found in SI Appendix.