High-Efficiency Multilevel Volume Diffraction Gratings inside Silicon

Abstract

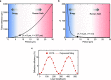
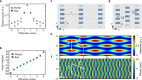
Silicon (Si)-based integrated photonics is considered to play a pivotal role in multiple emerging technologies, including telecommunications, quantum computing, and lab-chip systems. Diverse functionalities are either implemented on the wafer surface ("on-chip") or recently within the wafer ("in-chip") using laser lithography. However, the emerging depth degree of freedom has been exploited only for single-level devices in Si. Thus, monolithic and multilevel discrete functionality is missing within the bulk. Here, we report the creation of multilevel, high-efficiency diffraction gratings in Si using three-dimensional (3D) nonlinear laser lithography. To boost device performance within a given volume, we introduce the concept of effective field enhancement at half the Talbot distance, which exploits self-imaging onto discrete levels over an optical lattice. The novel approach enables multilevel gratings in Si with a record efficiency of 53%, measured at 1550 nm. Furthermore, we predict a diffraction efficiency approaching 100%, simply by increasing the number of levels. Such volumetric Si-photonic devices represent a significant advance toward 3D-integrated monolithic photonic chips.

Figure 1

(a) Schematic representation of multilevel laser patterning inside Si and optical characterization of volume gratings. The laser beam on the right (λ = 1550 nm) is used for 3D patterning, while the beam on the left represents a continuous-wave laser (λ = 1550 nm) used for measuring the grating diffraction efficiency. (b) A representative array of 21 experimental images acquired on x–y planes shows the progress of diffraction orders along the z-axis. For ease of visualization, a laser wavelength of λ = 1310 nm is used for imaging. The data are recorded on 200 μm-separated planes over a distance of 4 mm. (c) The SEM image of the sample cross section confirms multilevel subsurface fabrication in Si. Inset: a close-up view from the middle level, revealed after brief chemical etching.

Figure 2

(a) Dependence of the Talbot distance on the grating period, Λ. Grating operating regimes are shown in the background with colors. (b) The parameter ρ is plotted against the grating period. Grating operates in the Raman-Nath regime for ρ ≤ 1, whereas large values of ρ (ρ ≫ 1) correspond to the Bragg regime. An intermediate regime between these two distinct cases is observed for 1 < ρ < 10. In experiments, ρ = 5.4 and c = 287 μm are chosen. (c) FDTD simulation shows the dependence of DE on the length of single-level grating with a period of 8 μm. The simulation assumes a normal incidence. A sinusoidal modulation of diffraction efficiency is observed, with a peak value of 10%. Duty cycle of 50% is assumed in panels (a)–(c).

Figure 3

(a) Relative power, theoretical versus experimental, carried by the diffraction orders of a single-level grating created by using the parameters in Table 1. (b) Angular distribution of the diffraction orders from the same grating is determined by the grating equation and compared with measurements. (c, d) Schematic illustrations of the multilevel grating designs. The schematics show three levels along the z axis, but up to five levels have been fabricated in Si and reported in the paper. (c) Laterally aligned grating array design: levels are aligned with respect to each other and separated by the Talbot plane separation c in the z direction. (d) Proposed laterally shifted grating array design: levels are shifted by half period Λ/2 along the y axis, in relation to the levels before and after them and separated by c/2, half the Talbot plane separation, in the z direction. (e, f) Near-field intensity and phase distributions generated by interference of three beams that represent the 0 and ±1 orders of a 5-level grating with Λ = 3.2 μm. The relative power in the three orders is calculated by FDTD modeling. Higher diffraction orders can be ignored for the emergence of the Talbot self-imaging effect. The basis vectors of the optical lattice are also superposed over intensity and phase patterns (c: Talbot plane distance; Λ: grating period).

Figure 4

(a–c) Electric-field intensity distributions in the near-field for various single- and multilevel architectures. The outer black frames represent the 2D simulation area, while the inner rectangular blocks represent the laser-written regions, which form the distinct levels of the grating. The length of the simulation area along the y axis is equal to one period of the grating, which is repeated with the periodic boundary condition in simulations. The electric-field intensity distributions presented in panels (a)–(c) belong to single-level, laterally aligned 4-level, and laterally shifted 5-level gratings, respectively. (d) Combined first-order diffraction efficiency as a function of center-to-center (c-to-c) separation for a 2-level grating in Si. (e, f) Theoretical and experimental combined first-order efficiency values as a function of the number of distinct levels for the (e) laterally aligned and (f) laterally shifted grating designs in Si. All computations assume the grating parameters given in Table 1.